Generalizing distinguishability of photons on HOM dip?

[Cleber]

Hello all. I am trying to determine what is the effect of having photons that are distinguishable undergoing a quantum interference process. To do that, I try to generalize the Hong-Ou-Mandel effect, and try to determine what are the terms that appear as a function of the product of the creation operators at the output ports of a Directional Coupler (DC). DCs are integrated waveguide beam-splitters with a Unitary Operator U_DC as in Fig.1 below.

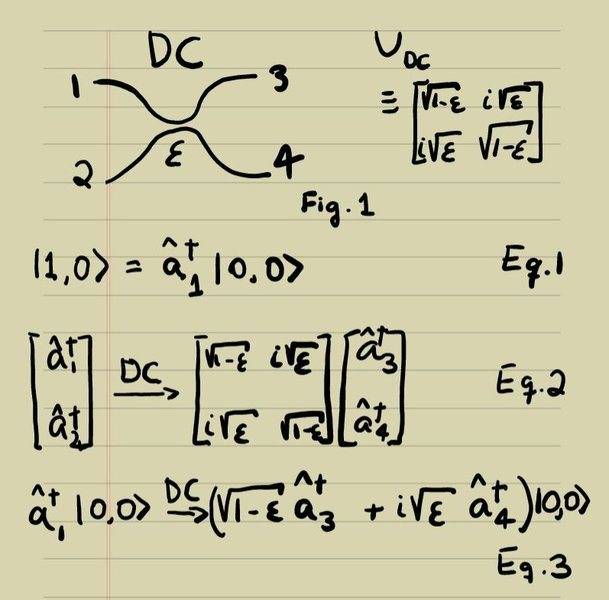
A single photon input at port 1 transforms into a combination of creation operators at output ports 3 and 4, which determine the respective probability of detection according to Eq. 3.
In Eq.3, ε is the coupling factor between the DC waveguides, generally 1/2 for a 50:50 beam-splitter.

Next, I consider a generic Unitary Operator U₁ (Eq. 4) on the photon before entering the DC (Fig. 2).

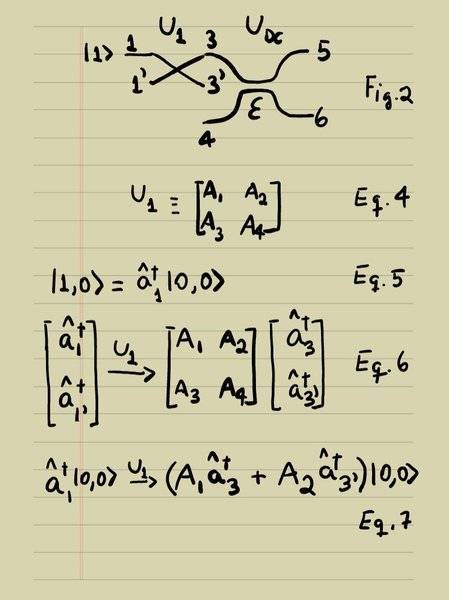
Now, a single photon at new input port 1 transforms into a combination of creation operators at output ports of U₁, port 3 and 3', according to Eq. 7.

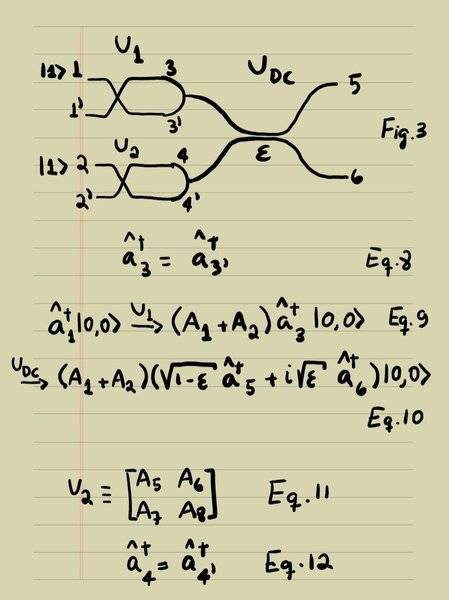
If ports 3 and 3' are combined, what can be done with waveguides or optical fibers, as in Fig. 3, their creation operators become identical (Eq. 8). Eq. 7 then becomes Eq. 9. The single photon at input port 1 is then transformed, at output ports 5 and 6 of DC, according to Eq. 10.

Now, I do the same for the other input port of DC, transforming the second photon of an identical photon pair, according to another generic Unitary Operator U₂ (Eq. 11).

Eqs. 9 and 10 then become, for this second photon, Eqs. 13 and 14 respectively.

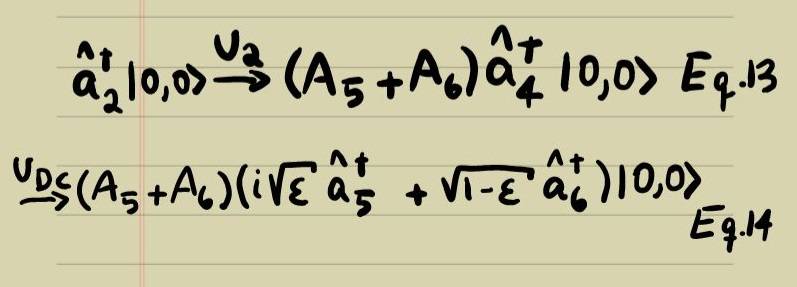
The idea is to try determining what is the effect of U₁ and U₂ on the final probability of simmultaneous counting of identical photon pairs at coincidence detectors in output ports 5 and 6. This simmultaneous counting probability is proportional to the multiplier of terms containing a product of creation operators at 5 and 6, according to Eq. 16.

These multipliers should contain a function of U₁ and U₂, to account for the increace of distinguishability of photons in case U₁ and U₂ are different. And here is the problem, since the coincidence probability seems to become zero if ε is 1/2, independently of U₁ and U₂ (Eq. 17). I am definitely missing something here! Can anybody tell me what is wrong?

 

[Swamp Thing]

I don't know much about optical waveguides, but I've worked with microwave directional couplers, and I would guess that a lot of the fundamental principles would be the same.

What strikes me is that you are trying to merge the waves emerging from 3 and 3' in figure 3, sending them to the input of the DC. When we do that, we have to consider the possiblility that some energy will flow back towards the left, and end up at 1'. Some of it could also end up at 1 in the form of a poor return loss. I assume you are taking care of the impedance matching between 3 and 3' (which are sort of 'in parallel') with the input of U_DC. But you need to check whether perfect return loss AND perfect isolation between 1 and 1' can be consistent with reciprocity and conservation of energy etc.