n7imo
- 7
- 2
Hello,
A friend of mine gave me this puzzle and I'd like to share it with you, math enthusiasts:
Two ladders intersect in a point O, the first ladder is 3m long and the second one 2m. O is 1m from the ground, that is AC = 2, BD = 3 and OE = 1 (see the image bellow)
Question: what's the value of DC ?
Note:
E is the perpendicular projection of O on [DC] and it does not necessarily divide [DC] in two equal parts.
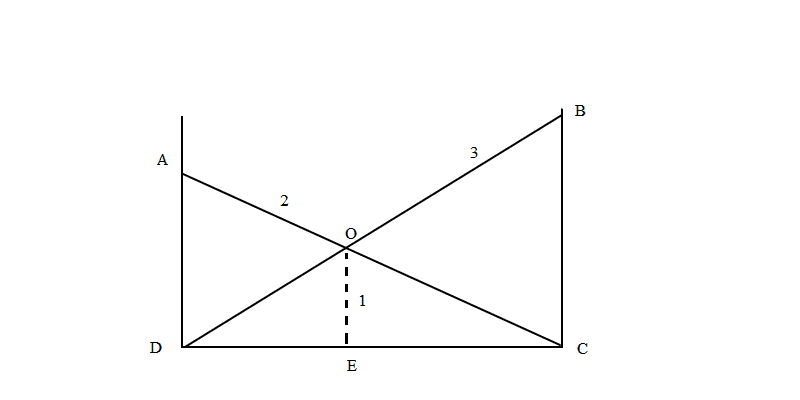
A friend of mine gave me this puzzle and I'd like to share it with you, math enthusiasts:
Two ladders intersect in a point O, the first ladder is 3m long and the second one 2m. O is 1m from the ground, that is AC = 2, BD = 3 and OE = 1 (see the image bellow)
Question: what's the value of DC ?
Note:
E is the perpendicular projection of O on [DC] and it does not necessarily divide [DC] in two equal parts.