Alex126
- 84
- 5
Moved thread to homework forum
There are three "concentric" rectangles, one inside the other, like in this figure:
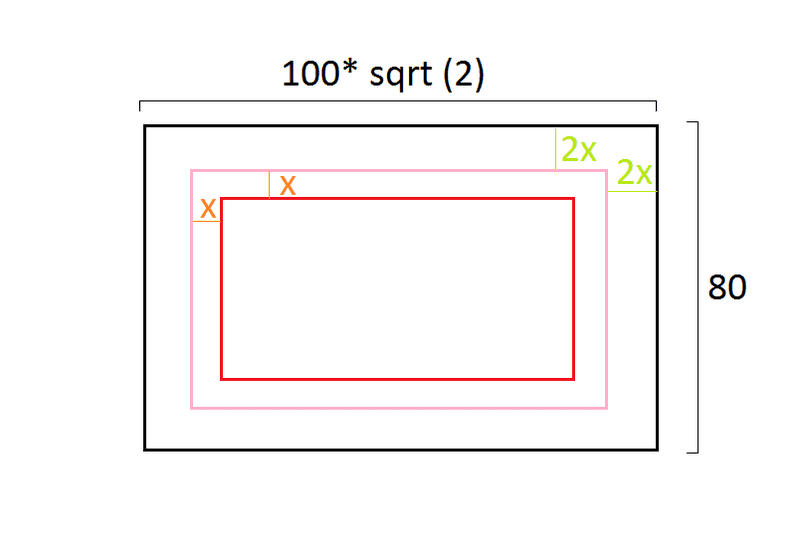
The image is not perfect, but we know that the distance between the sides of the inner-most rectangle and the middle rectangle is always "X", while the distance between the middle rectangle and the outer rectangle is equal to 2X.
The outer-most rectangle has sides of these measurements: 80; 100*√2
The inner-most rectangle has an area of: 5600*√2 - 4200
Calculate X.
The way I tried to solve it was with an equation, by working on the area of the inner-most rectangle. Since its sides should be equal to the outer-rectangle sides minus a total of 6x, then we can say:
(80-6x)*(100*√2 - 6x) = 5600*√2 - 4200
I confirmed with wolfram alpha that this equation would give me the correct solution (5√2). It also gives another solution, which is geometrically incompatible (X would be too big to be a smaller part of the bigger triangle). So if it wasn't logically clear enough, I have the "mathematical evidence" that I haven't done anything wrong.
However, the problem is that when I go and try to solve the equation, it becomes an awful mess of numbers which are incompatible with the typical level of difficulty of the exercises found on the textbook where this exercise comes from. The last passage before using the formula to solve the equation is:
3*x2 - (40+50√2) x + (200√2 + 350) = 0
I double-checked on wolfram alpha again, and it's all good to give the solution 5√2.
However, I can't seem able to figure how to actually do the maths and calculate it by myself. The Δ I get is 10800 - 400√2, and I'm stuck there. I can extract the 400, but I'm still left with 20* √(27-√2) afterwards.
Is there another way to set and solve the problem? If not, how am I supposed to solve the equation with basic high-school maths?
The image is not perfect, but we know that the distance between the sides of the inner-most rectangle and the middle rectangle is always "X", while the distance between the middle rectangle and the outer rectangle is equal to 2X.
The outer-most rectangle has sides of these measurements: 80; 100*√2
The inner-most rectangle has an area of: 5600*√2 - 4200
Calculate X.
The way I tried to solve it was with an equation, by working on the area of the inner-most rectangle. Since its sides should be equal to the outer-rectangle sides minus a total of 6x, then we can say:
(80-6x)*(100*√2 - 6x) = 5600*√2 - 4200
I confirmed with wolfram alpha that this equation would give me the correct solution (5√2). It also gives another solution, which is geometrically incompatible (X would be too big to be a smaller part of the bigger triangle). So if it wasn't logically clear enough, I have the "mathematical evidence" that I haven't done anything wrong.
However, the problem is that when I go and try to solve the equation, it becomes an awful mess of numbers which are incompatible with the typical level of difficulty of the exercises found on the textbook where this exercise comes from. The last passage before using the formula to solve the equation is:
3*x2 - (40+50√2) x + (200√2 + 350) = 0
I double-checked on wolfram alpha again, and it's all good to give the solution 5√2.
However, I can't seem able to figure how to actually do the maths and calculate it by myself. The Δ I get is 10800 - 400√2, and I'm stuck there. I can extract the 400, but I'm still left with 20* √(27-√2) afterwards.
Is there another way to set and solve the problem? If not, how am I supposed to solve the equation with basic high-school maths?