EebamXela
- 16
- 0
Back in november I asked the forum about this fractal:
http://en.wikipedia.org/wiki/File:Phi_glito.png
At the time I couldn't figure out how to make it.
Since then I've figured it out. I used MS Excel.
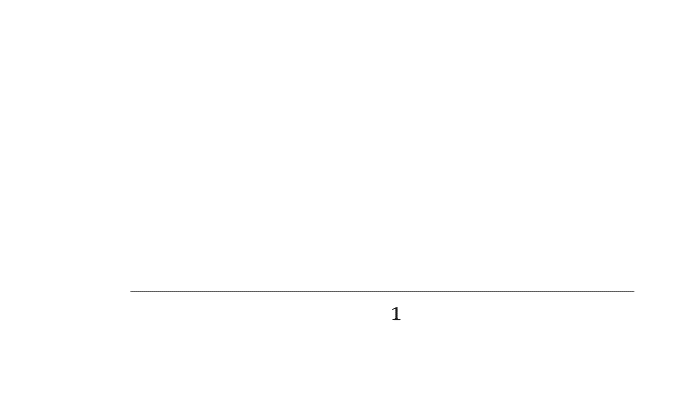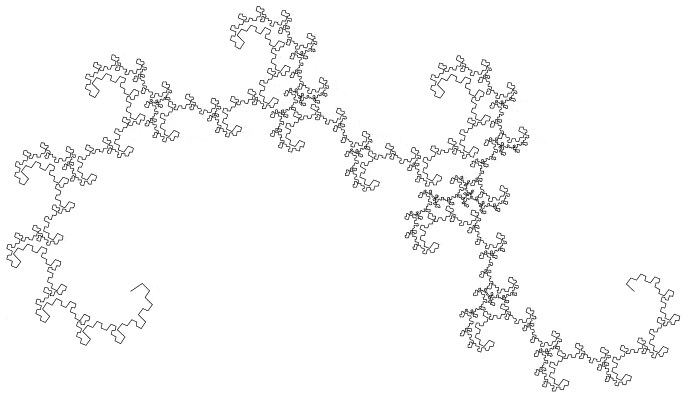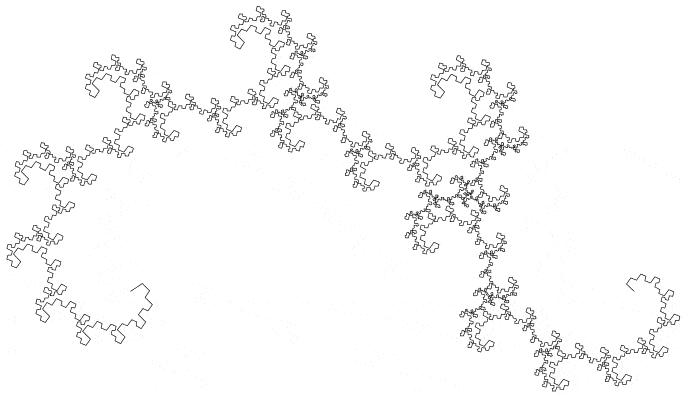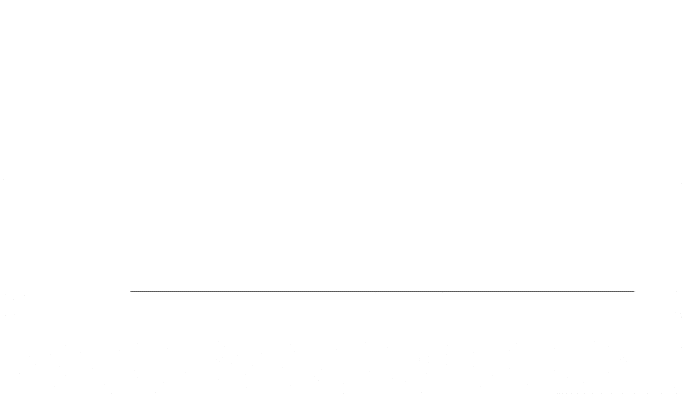
I'm not completely satisfied though. There are some gaps between the major portions of the fractal that I'm pretty sure are a result of the limited precision of Excel. I'm not so good with coding, so I just brute forced it with the only program i know well.
Also, I was only able to iterate the fractal 18 times. My laptop was struggling hard to iterate the final step and even failed several times to do so. Excel crashed like 4 times in the middle of calculating. So i think a 19th is out of the question given my limited abilities.
Hi resolution:
http://i.imgur.com/lKXzIBH.jpg
http://en.wikipedia.org/wiki/File:Phi_glito.png
At the time I couldn't figure out how to make it.
Since then I've figured it out. I used MS Excel.
I'm not completely satisfied though. There are some gaps between the major portions of the fractal that I'm pretty sure are a result of the limited precision of Excel. I'm not so good with coding, so I just brute forced it with the only program i know well.
Also, I was only able to iterate the fractal 18 times. My laptop was struggling hard to iterate the final step and even failed several times to do so. Excel crashed like 4 times in the middle of calculating. So i think a 19th is out of the question given my limited abilities.
Hi resolution:
http://i.imgur.com/lKXzIBH.jpg