Graph States for Quantum Secret Sharing

[limarodessa]

In Graph States for Quantum Secret Sharing on page 3 :

‘…The “encoded graph state” is $$\left| {{G_{{{\vec l}_{*2}}}}} \right\rangle = \mathop \otimes \limits_i Z_i^{{l_{i2}}}\left| G \right\rangle $$ . (3.9) …

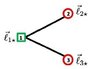
Example 1. The three-qubit labeled graph state presented
in Fig. 1 is the encoded graph state

$$\left| {{G_{{{\vec l}_{*2}}}}} \right\rangle = Z_1^{{l_{12}}} \otimes Z_2^{{l_{22}}} \otimes Z_3^{{l_{32}}}\left( {\frac{{\left| {0 + + } \right\rangle + i\left| {1 - - } \right\rangle }}{{\sqrt 2 }}} \right)$$ , (3.13) …’

I understand that $$\mathop \otimes \limits_i Z_i^{{l_{i2}}} = Z_1^{{l_{12}}} \otimes Z_2^{{l_{22}}} \otimes Z_3^{{l_{32}}}$$

But I don’t understand why $$\left| G \right\rangle = \left( {\frac{{\left| {0 + + } \right\rangle + i\left| {1 - - } \right\rangle }}{{\sqrt 2 }}} \right)$$

I ask explain to me – why it is so

 

[DonQubito]

It might just be a typo. From definition 3, \left( \left|0++\right>+i\left|1--\right> \right)/\sqrt{2} [\itex] is supposed to be the graph state \left| G \right>[\itex]. If I am correct in that assumption then \left|G\right> [\itex] cannot have any imaginary amplitudes. This is because you can create the graph by doing a series of controlled phases, one for each edge of the graph, to the state \left|+\right>^{\otimes 3}[\itex]. Controlled phases can only change the phase of a computational basis state by -1[\itex].