Fatima Hasan
- 315
- 14
Homework Statement
Identify the particle's path by finding a Cartesian equation for it . Graph the Cartesian equation . indicate the portion of the graph traced by the particle .
##x=2sinh t## , ##y=2cosh t## , ##-\infty < t < \infty##
Homework Equations
##cosh^2 t - sinh^2 t = 1##
The Attempt at a Solution
##sinh t = \frac{x}{2}##
Square both sides :
##sinh^2 t = \frac{x^2}{4}## (1)
##cosh t = \frac{y}{2}##
Square both sides :
##cosh^2 t = \frac{y^2}{4}## (2)
(2) - (1) :
##cosh^2 t - sinh^2 t = 1##
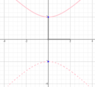
##\frac{y^2}{4} - \frac{x^2}{4} = 1##
put x= 0 → y=±2
Is my answer correct ?
Attachments
Last edited: