Graphical to Mathematical representation of changing the order of some elements

[arsenal_51]

I have a question that is a little hard to explain, since i don't know the name of this method, but I'll try my best, if anyone knows the name please do tell me.

So let's say we have three numbers, 1 2 3 (in this order)
and we have a container for this numbers: C₁₂₃
and we have some operations: O₁₂, O₁₃ and O₂₃
each of these operations act on those numbers changing their positions.

For example O₁₂ will change the position of the first and second elements.
So let's say: O₁₂ . C₁₂₃ will equal: C₂₁₃

And if we want to find out what operations to use when we have the original Container and the target Container we can do it easily graphically.
For example:
Original: C₁₂₃
Target: C₂₃₁

This can be done graphically:

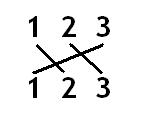
The point where the lines intercept represent the operation between those two numbers. And the order is important, since these operations are not commutable.

So that's the same as: O₁₂ . O₂₃ . C₁₂₃ = C₂₃₁


One last example:
The container doesn't need to hold all of the numbers of the three number-space
Original: C₁₂
Target: C₃₁

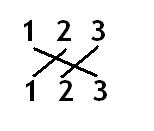
Or: O₂₃ . O₁₂ . C₁₂ = C₃₁


So graphically its easy to find out the operations of any N number-space.
But how do we express that in a mathematical general expression?

 

[Number Nine]

I'm not exactly sure what you're asking. These are just basic permutations, so cycle notation should communicate everything that you need.

 

[arsenal_51]

Thanks for your reply, I'm going to read about that.

I'm trying to find out the permutations needed to do mathematically for any N number group, knowing only the original and the final state.
Ideally something of the format: O_1i . O_2j . C₁₂ = C_ij
But for a N number group instead of just a this small example that might not even be correct.

 

[Michael Redei]

Thanks for your reply, I'm going to read about that.

I'm trying to find out the permutations needed to do mathematically for any N number group, knowing only the original and the final state.
Ideally something of the format: O_1i . O_2j . C₁₂ = C_ij
But for a N number group instead of just a this small example that might not even be correct.

Your notation is somewhat unconventional, but I think you mean the following: Given an ordered set of the first N counting numbers, i.e. $S = (s_1\,s_2\,s_3\,\ldots\,s_N)$, you want to find $X$ "swappings" of the form $(f_1\,t_1),\ldots,(f_X\,t_X)$ such that their product will take the ordered set $(1\,2\,3\,\ldots\,N)$ to $S$, i.e.
$$
(1\,2\,3\,\ldots\,N)\cdot(f_1\,t_1)\cdot\ldots \cdot (f_X\,t_X)=(s_1\,s_2\,s_3\,\ldots\,i_N).
$$
This is possible, and you can construct the pairs $(f_k\,t_k)$ quite easily. I'll just hint by saying this much: choose $(f_1\,t_1)$ so that it swaps the elements $1$ and $s_N$, and then let $(f_2\,t_2)=(1\,N)$. This means that those two swapping put $s_N$ at position $N$. In the next step you place $s_{N-1}$ into position $N-1$ etc. till you end up with the ordered set $S$ you wanted.

This way you may need $X=2N-1$ swappings, and it's actually possible to get from $(1\,2\,3\,\ldots\,N)$ to any $(s_1\,s_2\,s_3\,\ldots\,s_N)$ with only $N-1$ swappings, but not as easily as by my method (one element at a time goes into position $1$ and then to its proper place).

 

[arsenal_51]

Thank you, i will try out your method, it seems pretty clear.

After i try that out i would like to check that other more efficient method you were talking about where you only need N - 1 swapping operations. Do you know where i can read more about that other method or the name of it?

Thanks again.