arsenal_51
- 3
- 0
I have a question that is a little hard to explain, since i don't know the name of this method, but I'll try my best, if anyone knows the name please do tell me.
So let's say we have three numbers, 1 2 3 (in this order)
and we have a container for this numbers: C123
and we have some operations: O12, O13 and O23
each of these operations act on those numbers changing their positions.
For example O12 will change the position of the first and second elements.
So let's say: O12 . C123 will equal: C213
And if we want to find out what operations to use when we have the original Container and the target Container we can do it easily graphically.
For example:
Original: C123
Target: C231
This can be done graphically:
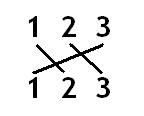
The point where the lines intercept represent the operation between those two numbers. And the order is important, since these operations are not commutable.
So that's the same as: O12 . O23 . C123 = C231
One last example:
The container doesn't need to hold all of the numbers of the three number-space
Original: C12
Target: C31
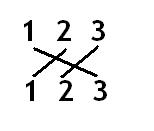
Or: O23 . O12 . C12 = C31
So graphically its easy to find out the operations of any N number-space.
But how do we express that in a mathematical general expression?
So let's say we have three numbers, 1 2 3 (in this order)
and we have a container for this numbers: C123
and we have some operations: O12, O13 and O23
each of these operations act on those numbers changing their positions.
For example O12 will change the position of the first and second elements.
So let's say: O12 . C123 will equal: C213
And if we want to find out what operations to use when we have the original Container and the target Container we can do it easily graphically.
For example:
Original: C123
Target: C231
This can be done graphically:
The point where the lines intercept represent the operation between those two numbers. And the order is important, since these operations are not commutable.
So that's the same as: O12 . O23 . C123 = C231
One last example:
The container doesn't need to hold all of the numbers of the three number-space
Original: C12
Target: C31
Or: O23 . O12 . C12 = C31
So graphically its easy to find out the operations of any N number-space.
But how do we express that in a mathematical general expression?