- #1
songoku
- 2,294
- 325
- Homework Statement
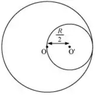
- A planet of mass ##M## has a part of it removed as shown in the diagram. Find the gravitational field at point A (which is 1/2 R from O) and point B (which is 2R from surface)
- Relevant Equations
- ##g=\frac{GM}{r^2}##
##g=\frac{GM}{R^3}r##
##V=-\frac{GM}{r}##
The removed mass is ##\frac{1}{8}M##
My idea is to find ##g## from large sphere then minus it with ##g## from small sphere (because of the removed mass):
##g## at A =
$$\frac{GM}{R^3}\left(\frac{1}{2}R\right)-\frac{G\left(\frac{1}{8}M\right)}{R^2}$$
Is this correct? Thanks