I Gravitational lensing: deriving magnification of lensed image

[astrostudent21]

TL;DR Summary

In gravitational lensing, the image magnification is defined as the image size over the source size. But many texts also give it as the determinant of the jacobian of the of the lens equation. How are these equivalent?

In gravitational lensing, the image magnification is defined as the image area over the source area. But many texts also give it as the inverse of the determinant of the jacobian, A, of the of the lens equation. My question is how these are equivalent.

The lens equation is β=θ-α(Dlens-source)/(Dlens)
The jacobian that describes it is then

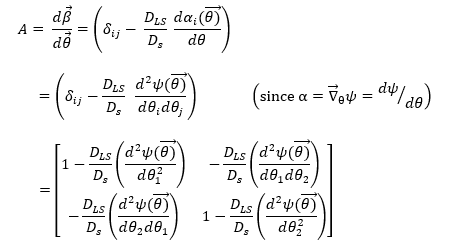
many texts say that we can calculate the magnification as μ=1/det[A], but I have not found one that actually derives this relation from the initial definition of the magnification as the ratio of the image and source areas. I would really appreciate help from anyone who has experience with this topic!

 

[George Jones]

Summary:: In gravitational lensing, the image magnification is defined as the image size over the source size. But many texts also give it as the determinant of the jacobian of the of the lens equation. How are these equivalent?

Have you looked at pages 63 - 65 in the book "Gravitational Lensing" by scott Dodelson? I was able to use the LOOK INSIDE! feature of Amazon to look at these pages.

 

[astrostudent21]

Have you looked at pages 63 - 65 in the book "Gravitational Lensing" by scott Dodelson? I was able to use the LOOK INSIDE! feature of Amazon to look at these pages.

Thank you so much for pointing me towards that book. I suppose what I was overlooking was that the image area over the source area is really the same thing as d^2(θ)/(dβ)^2 . I think I am on the right track now.

EDIT: Hmmm... actually I am not quite following the logic here. If mu = d^2(θ)/(dβ)^2, and dβ/dθ given by the matrix A, it seems to me that mu = (A^-1)^2, not det(A)^-1. I am not seeing where the determinant comes in. Am I missing something?