NeedFreedom
- 5
- 1
- TL;DR
- Machine prototype needs some physics and math input from those in the know
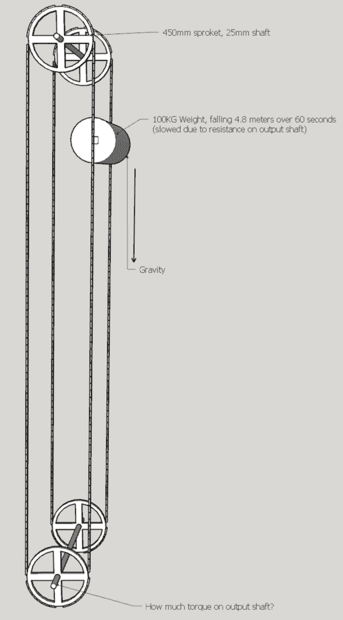
Im prototyping a machine to lower liquid from a height using a chains and sprockets. Essentially liquid will fill at top, be lowered over a distance of 4.8 metres then emptied at bottom. The liquid needs to be lowered at a slow pace due to resistance on the output shaft, I am considering utlising an alternator to provide resistance and convert rotational torque into electricty. I need to work out the forces involved and need some help with the math!
I have put together a basic model with the variables/inputs and would like some help figuring out the following:
Whats the relationship between weight, gravity, speed, losses and output shaft torque?
To achieve 70NM torque on output shaft, how much weight is needed?
What are the calculations for this problem?
Let me know if questions and more info needed, and thanks for any help in advance!
I have put together a basic model with the variables/inputs and would like some help figuring out the following:
Whats the relationship between weight, gravity, speed, losses and output shaft torque?
To achieve 70NM torque on output shaft, how much weight is needed?
What are the calculations for this problem?
Let me know if questions and more info needed, and thanks for any help in advance!
Last edited by a moderator: