Kingpin1880
- 1
- 0
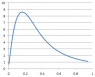
I'm not 100% sure if this question has been asked/answered or not but I was curious about this subject and I fear I'm not knowledgeable enough to figure out this question for myself. I know that the gravity at the surface of the sun is roughly 28g, but as gravity gets more intense the closer to the centre of mass of the celestial body in question; how strong would gravity be closer to / within the core?
I'll be happy with a rough estimate if it's a bigger question than I think it is; I fell out of love with the study of science after high school, but I still think it a fascinating subject.
(here's hoping I didn't sound pretentious... also; not sure what "prefix" to use so sorry if this question's in the wrong place)
I'll be happy with a rough estimate if it's a bigger question than I think it is; I fell out of love with the study of science after high school, but I still think it a fascinating subject.
(here's hoping I didn't sound pretentious... also; not sure what "prefix" to use so sorry if this question's in the wrong place)