Waxterzz
- 82
- 0
Hi all,
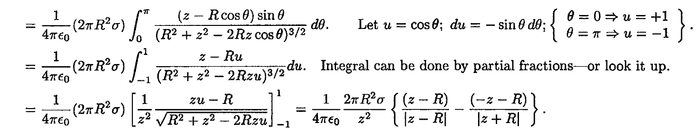
"Integral can be done by partial fractions - or look it up" So second line, that's what I want to do.
How to deal with this? What substitution can I use? Never encountered partial fractions with non-integer exponents.
Someone give me a tip?
Thanks in advance
"Integral can be done by partial fractions - or look it up" So second line, that's what I want to do.
How to deal with this? What substitution can I use? Never encountered partial fractions with non-integer exponents.
Someone give me a tip?
Thanks in advance