edfink1
- 3
- 5
- Homework Statement
- Griffiths Quantum Mechanics 2nd edition
- Relevant Equations
- Griffiths second edition equations 8.24 and 8.25
In Griffiths Quantum Mechanics 2nd edition, in Chapter 8 he calculates the following integral on page 323
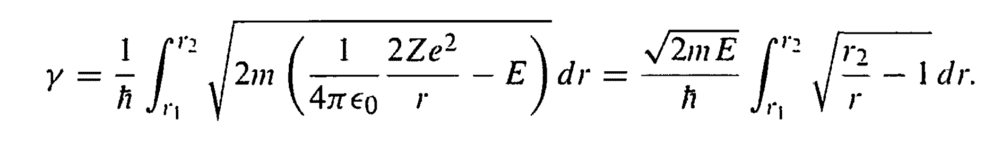
and he gets
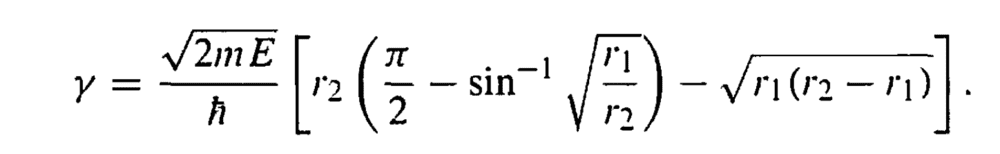
I disagree with this result, I think the integral should be
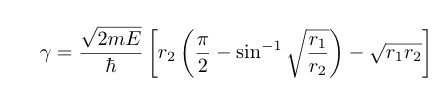
since
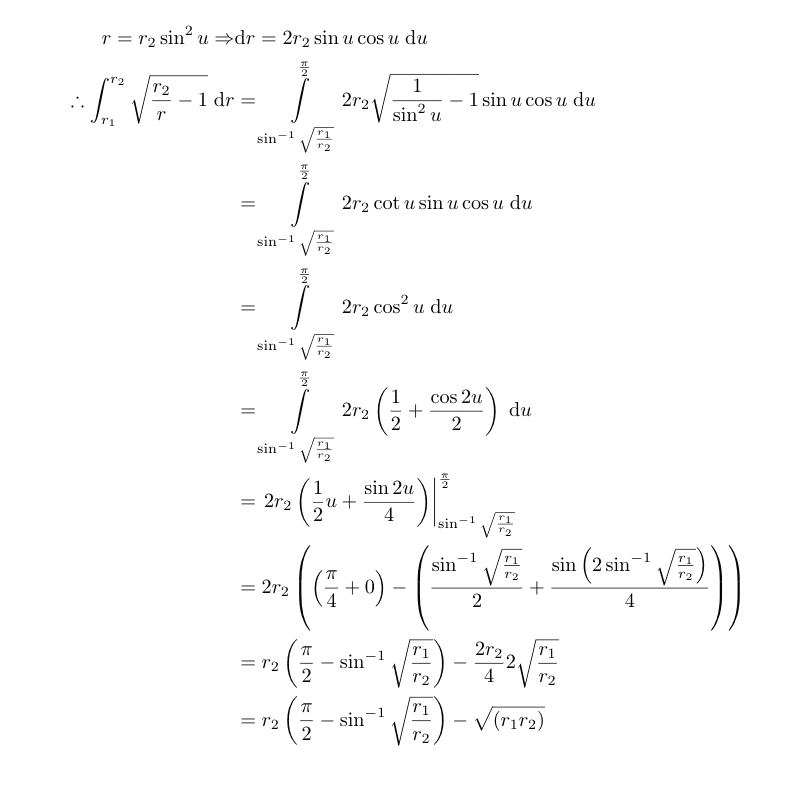
Maybe somebody can explain why I am wrong? Also, from equation 8.24 to 8.25, he makes the assumption that sinϵ ≅ ϵ, but how does that imply sin^(-1)ϵ ≅ ϵ, which seems to be what he assumes to get from 8.24 to 8.25. Any insight is greatly appreciated!
and he gets
I disagree with this result, I think the integral should be
since
Maybe somebody can explain why I am wrong? Also, from equation 8.24 to 8.25, he makes the assumption that sinϵ ≅ ϵ, but how does that imply sin^(-1)ϵ ≅ ϵ, which seems to be what he assumes to get from 8.24 to 8.25. Any insight is greatly appreciated!