Ground faults in ungrounded systems

[DavBav1]

HiThis is most likely a stupid question, but sometimes I have to ask them...
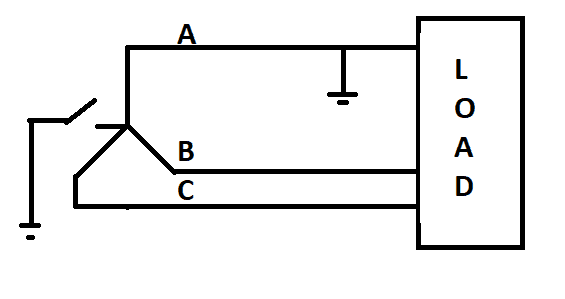
Imagine the following circuit shown in the image below; there is a ground fault in phase A and let's say the fault impedance is zero.

Because of this fault; the potential, with respect to ground, of phase A is zero.
I'm however not able to tell/undestand: What happens with the line currents after the fault, how will they change?

The load/equipment will still operate, as this is one of the benefits of ungrounded system, that the phase to phase voltages remains the same after the fault.

Thanks, any help is greatly appreciated.

 

[.Scott]

If there is no other connection to ground - either resistive, capacitive, or inductive, then there will be no change to the currents.

I have to add: It all depends on what we are describing, but once line A contacts ground then it is possible that the equipment would become less safe.

 

[DavBav1]

Hi,

Ok, so in real life the ungrounded system is grounded via its capacitance to earth.

I found this picture on the web (see below), going back to my original image in post #1: Can we say that the currents with the fault will be the same as before, but phase A has the additional capacitative current?

And I assume this current is small, so small changes in line currents basically?

 

[Babadag]

In my opinion, generally speaking, this diagram is better.

Usually, since Xxfr <<XC you may neglect the transformer impedance [also R and L of the line] and so the charge capacitive current will be:
Igf=ω*Cn*VL_L/sqrt(3) where:
ω=2.п.f=314.16 for 50 Hz
Cn=2*п*ε/ln(D/d) ε= 8.85E-12 F/m
D=conductor centerline-to-centerline distance
d=conductor diameter.
VL_L line rated voltage [phase-to-phase]
For a 2/0 AWG [10 mm diameter] 1 m distance overhead line 35 kV 30km Igf=2 A but for the same conductor three-core cable Igf=30 A.
For higher voltage the current rise proportionally [approx.]

 

[DavBav1]

Thanks @Babadag

One question that came to mind: If I want to calculate the power of my circuit during ground fault, I can't use phase voltage because this is now zero, do I just use phase-phase voltage and divide by sqrt(3)? And multiply with current (load + ground fault).

 

[Tom.G]

One question that came to mind: If I want to calculate the power of my circuit during ground fault, I can't use phase voltage because this is now zero,...

Uhm,

• Did you forget about the resistance of the conductor(s) between the transformer and the short?
• How about the winding resistances of the transformer primary and secondary?
• How about core saturation?
• How about the resistance of the distribution lines supplying the primary?

Or is this a homework problem?

Cheers,
Tom

 

[DavBav1]

Hi,

Not a homework problem, just a newbie trying to understand :).

Fair enough, but consider the following schematic below.
If I measure voltages and currents at points located directly after the ground fault.
Now my phase to ground voltage measurement will read zero in phase Y.

How can I calculate the total power in an arbitrary phase now?
Sy = Uph*conj(Iph) will give me zero, because Uph is zero.

But I know the load will continue to work as normal, because its connected line to line and the system is "ungrounded", hence drawing power.

Thanks.

 

[Tom.G]

First, you can simplify your schematic by connecting the Gnd symbols with a wire; then eliminate the Gnd symbols. This is valid because all Gnd's by definition are the same point.

This will show that you have two capacitors in series between the "R" and "B" phases, essentially a capacitive voltage divider. The fact that they may be connected to the Earth is irrelevant, there is only one place for the current from either of them to go: the other capacitor.

Unless either Voltage or Capacitance are infinite, there is a finite, measurable, current flowing. The voltage at the junction of the capacitors (the point that used to be Gnd), measured to one of the phases, depends on the ratio of the capacitor values, and of course the phase voltages.

Also, the current available at the capacitor junction depends on the applied voltage, its frequency, and the capacitors values.

Hope this helps.

Cheers,
Tom

 

[jim hardy]

I found this picture on the web (see below), going back to my original image in post #1: Can we say that the currents with the fault will be the same as before, but phase A has the additional capacitative current?

And I assume this current is small, so small changes in line currents basically?

The simple answer to that question is "Yes" .
I really recommend you get a copy of "IEEE Green Book", standard 142.
Its early chapters explain clearly the basic principles on which the practice of grounding is built.
Familiarity with it makes a lot of the mysteries of the NEC disappear.
Once you train your brain to think of "ground" as just another wire that goes most everywhere these mysteries become almost intuitive.

But I know the load will continue to work as normal, because its connected line to line and the system is "ungrounded", hence drawing power.

Yes your load current is hopefully so large compared to your capacitive current that the system operates, to all outward appearance, normally .
So it's tempting to make industrial systems ungrounded to promote fault tolerance.
But you need detection of that first fault because should a second one come along on a different phase, now you have a dead short and two electrical explosions one at each fault.

IEEE Green Book's first few chapters explains all this, at length in plain language , then the authors go into extreme detail .

In the real world of industry we approximate an ungrounded system by grounding it through a considerable resistance - roughly equal to the capacitive reactance of the distributed system.
There's a clever reason for doing that, namely the phenomenon of "ferroresonance".
Should an inductance in the system, say a motor or transformer winding, happen to make a series resonant circuit with that distributed capacitance ,
well,
do you recall from your basic circuits course that the voltage gain of a series resonant circuit is its Q, which is its X/R? Ratio of energy stored to energy dissipated per cycle?( see wikipedia's entry for Q_factor )

That can really happen and the high voltages produced by resonance will pierce the insulation.
So we place some R across the X_C to prevent a high Q resonant situation.

And we monitor for presence of an unwanted ground so we can dispatch maintenance people to find and fix it before a second one comes along and disables the system.

And that's why Grounding is such an important subject.
As always the basics are straightforward. An appreciation of them will justify the highfalutin mathematical treatment given the subject elsewhere.

I said in another thread some years ago,

I feel that every EE curriculum should have a 1 credit hour course on IEEE 142, Green Book.
That so many electrical engineers graduate lacking understanding of "Ground" should be an embarrassment to the profession.
Just look at the questions we get here on PF about it.

That's my opinion.

I hope you'll become the 'resident expert' in your outfit.
You'll get a lot of mileage out of your basics..
Good luck in your career -

old jim

 

[DavBav1]

Thanks all.

I have one last question, and I'm sure I should have been able to figure this one out by myself, but I'm not...

During a single line to ground fault, the voltage across the healthy phases increase to line to line voltage. I.e. the voltage triangle remains intact, but the neutral point is shifted.

I'm not able to fully understad why, or show with eq's that this is true (I have seen it in real life, so I know it's true, that helps but still..)How should I start setting up my equations, to prove that the neutral point now is not at the same potential as ground?

My take at the problem without equations:
The voltage (130 V) across my Y phase coil, i.e. $V_{y}$, will be present even during a single line to ground fault.

But because the + side of my Y phase coil is now at ground potential, the potential of $V_{n}$ with respect to ground now has to be +130, i.e. the polarity of my Y coil shifts?

Is this the correct way of thinking, or am I simplifying things here?I really appreciate your help.

This quote explains well how I feel

The more I learn, the more I realize how much I don't know.

-Albert Einstein

 

[jim hardy]

This quote explains well how I feel

Yes, knowledge is humbling isn't it ? Appreciation of the abysmal depth of our ignorance is the beginning of wisdom...Yes you are basically correct in your analysis But you flipped a sign.
That's why we must be rigorous in applying Mr Kirchoff's gifts to us, 'the basics' .

It's important to remember that voltage is Potential Difference

Difference is a key concept - whenever you speak of voltage be sure to keep in mind between what two points.
It takes two points to define a voltage and that's why voltmeters always have two wires.

Develop that awareness early on and it'll prevent lots of confusion in your later studies.old jim