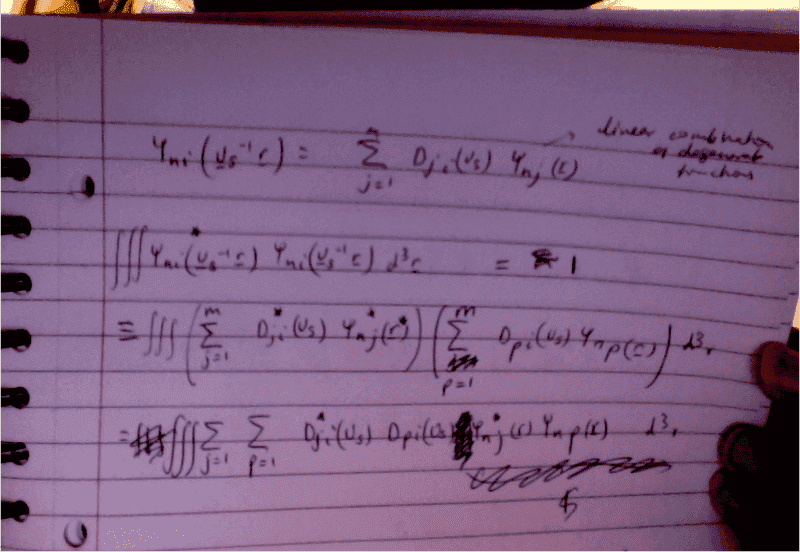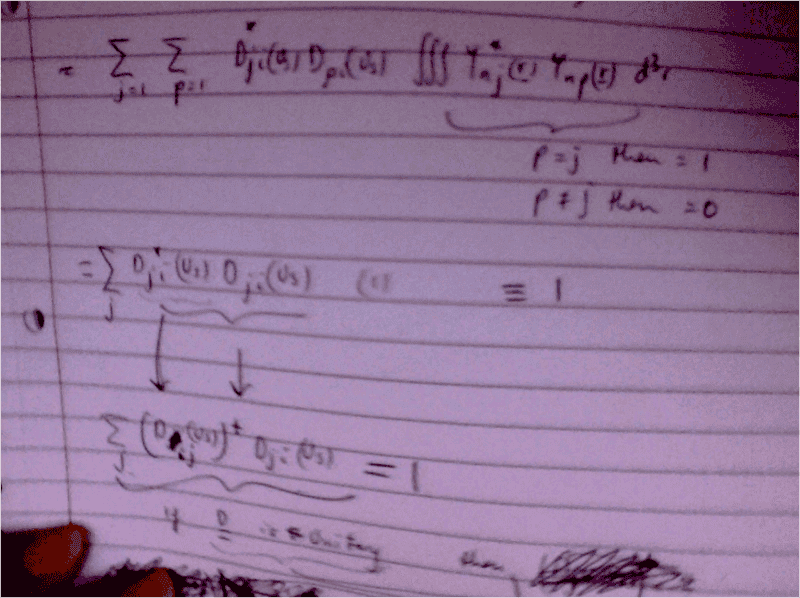SUMMARY
The discussion centers on the necessity of the matrix D being unitary in the context of quantum mechanics, specifically regarding the transformation of wavefunctions. The transformation is expressed as Tψ(r) = ψ(Ur) = ΣDij ψ(r), where Dij must maintain unitarity to preserve the lengths of vectors. The participants clarify that transformations do not inherently require unitarity unless they involve vector lengths, emphasizing the importance of this property in quantum state transformations.
PREREQUISITES
- Understanding of quantum mechanics and wavefunctions
- Familiarity with unitary matrices and their properties
- Knowledge of linear algebra, specifically matrix transformations
- Concept of vector lengths and their preservation in transformations
NEXT STEPS
- Study the properties of unitary matrices in quantum mechanics
- Explore the implications of transformations on wavefunctions in quantum theory
- Learn about representations in quantum mechanics and their mathematical foundations
- Investigate the role of vector length preservation in physical transformations
USEFUL FOR
Students and professionals in quantum mechanics, physicists focusing on wavefunction transformations, and mathematicians interested in linear algebra applications in physics.