c-murda
- 67
- 0
[SOLVED] Hanging masses and tensions...
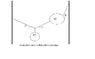
attached is drawing of diagram...
two masses m1 and m2 are attached as shown in the figure. If the system is in equilibrium, find the angle labled theta.
m1 = 35.0 kg
m2 = 65.0 kg
well...to start i drew three FBD one for the mass, one for the intersection, and one for the second mass...
for the first FBD:
Tm = m * g
for the second FBD:
Fx = T2 cos 53 - T1 cos 37 = 0
Fy = T2 sin 53 + T1 sin 37 - m1*g = 0
for the third FBD:
Fx = T3 cos (theta) - T2 cos 53 = 0
Fy = T3 sin (theta) - T2 sin 53 - m2*g = 0
so...
First:
Tm = m*g; which equals (35.0kg) ( 9.80 m/s^2) = 343N
Second:
.602 T2 - .799 T1 = 0 ; so... T1 = (.602/.799)(T2) so...
.602 T1 +.799 T2 = 343
.602[((.602)/(.799))T2 + .799 T2 = 343
.453T2 + .799T2 = 343
1.25T2 = 343
T2 = 274.4N
Third:
T3=T2(cos 53/cos (theta))
[T2(cos 53/cos (theta))] sin(theta) - T2 sin 53 = m2*g
T2 tan(theta) cos 53 = m2*g + T2 sin 53
tan(theta) = m2*g + T2 sin 53/T2 cos 53
theta = tan^-1(m2*g + T2 sin 53/T2 cos 53)
theta = 79.1?
uhmm any help? that's what i got correct me if i am wrong
Homework Statement
attached is drawing of diagram...
two masses m1 and m2 are attached as shown in the figure. If the system is in equilibrium, find the angle labled theta.
m1 = 35.0 kg
m2 = 65.0 kg
Homework Equations
The Attempt at a Solution
well...to start i drew three FBD one for the mass, one for the intersection, and one for the second mass...
for the first FBD:
Tm = m * g
for the second FBD:
Fx = T2 cos 53 - T1 cos 37 = 0
Fy = T2 sin 53 + T1 sin 37 - m1*g = 0
for the third FBD:
Fx = T3 cos (theta) - T2 cos 53 = 0
Fy = T3 sin (theta) - T2 sin 53 - m2*g = 0
so...
First:
Tm = m*g; which equals (35.0kg) ( 9.80 m/s^2) = 343N
Second:
.602 T2 - .799 T1 = 0 ; so... T1 = (.602/.799)(T2) so...
.602 T1 +.799 T2 = 343
.602[((.602)/(.799))T2 + .799 T2 = 343
.453T2 + .799T2 = 343
1.25T2 = 343
T2 = 274.4N
Third:
T3=T2(cos 53/cos (theta))
[T2(cos 53/cos (theta))] sin(theta) - T2 sin 53 = m2*g
T2 tan(theta) cos 53 = m2*g + T2 sin 53
tan(theta) = m2*g + T2 sin 53/T2 cos 53
theta = tan^-1(m2*g + T2 sin 53/T2 cos 53)
theta = 79.1?
uhmm any help? that's what i got correct me if i am wrong