Hat is the value of the second capacitor?

[liljediboi]

1. The electric field between the plates of a paper-separated (K(dielectric constant=3.75) capacitor is 9.21 x 10^4 V/m. The plates are 2.35 mm apart and the charge on each plate is .775 ìC. Determine the capacitance of this capacitor and he area of each plate.

2. A 6.5-microF capacitor is charged by a 125-V battery and then is disconnected from the battery. When it is then connected to a second (initially uncharged) capacitor, the voltage on the first drops to 10 V. What is the value of the second capacitor?

3. A 2.5-microF capacitor is charged to 1000 V and a 6.8-microF is charged to 650 V. The positive plates are now connected to each other and the negative plates are connected to each other. What will be the potentil difference across each and the charge on each?

** bonus question **

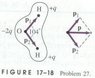
the dipole moment, considered as a vector, points from the negative to the positive charge. Water molecules have a dipole moment p which can be considered as the vector sum of the two dipole moments, p1 and p2. The distance between each H and the O is about .96 x 10^-10 m. The lines joining the center oof the O atom with each H atom make an angle of 104 degrees and the net dipole moment has been measured to be p = 6.1 x 10^-30 Cm. Determine the charge, q, on each H atom. (book provides a picture, which should be attatched)

thanks.

 

[himanshu121]

So in which part u have got doubt

 

[liljediboi]

need help on all

i need help with what happens when you disconnect the capacitor and connect to another. for the first question, i don't know how to manipulate the equations i know to make it solve, i always end up with capacitance and area and voltage as unknowns, i need one of those to solve, i think, as for the "bonus question" the answer i got does not agree with the back of the book

 

[pattiecake]

well capacitance=dielectric constant*(epsilon knot*Area)/distance of seperation, where epsilon knot is a constant = 8.85e-12. why don't you write out what work you have?

 

[liljediboi]

nvm, i got it, questions used concepts we haven't learned, or are in later chapters, so i looked for it.

useless book.