Help finding deflection of beam

[Dell]

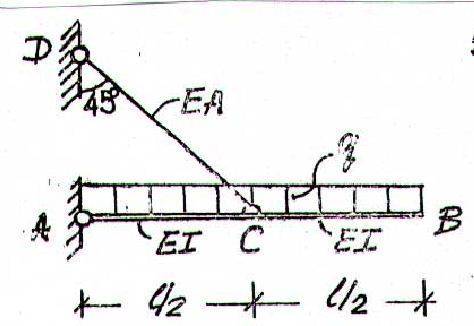
find the deflection of the beam at point B

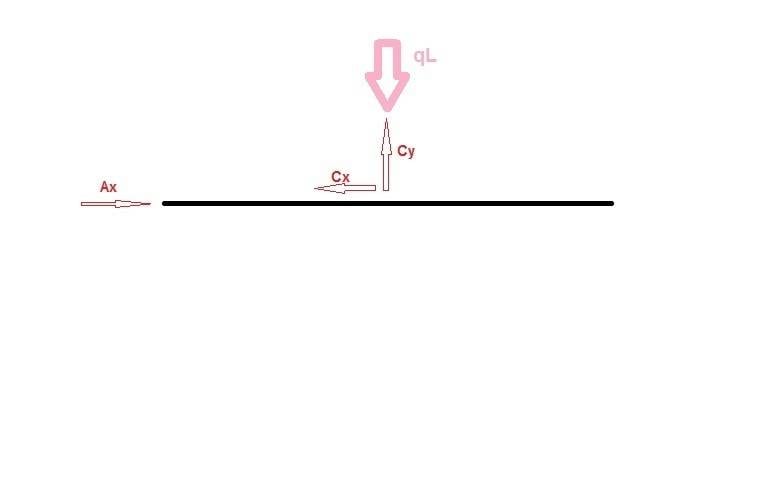
i drew the free body diagram of the beam and found that
Ay=0
Ax=qL
Cy=qL
Cx=qL

M(x)= (qL)*x - (qx)*x/2 +(qL)*<x-L/2>

M(x)=(qL)x -(q/2)x² +(qL)<x-L/2>

EIΦ(x)=(qL/2)x² -(q/6)x³ +(qL/2)<x-L/2>² + C1

EIY(x)=(qL/6)x³ -(q/24)x⁴ +(qL/6)<x-L/2>³ + C1*x + C2

EIY(0)=0= 0+ C2
===>c2=0

but i need another condition to find C1, i think i need to use the deflection of the bar DC somehow, but I am not quite sure how, i tried using triangles and saying that the deflection of point C is the same as the deflection of the bar DC*sin(45) but that didnt work

 

[pongo38]

There are 3 contributions to the deflection at B. Can you identify them? One of them is the extension of CD, as you have realized. If you know the force in CD, you should be able to work out its axial extension. By the way I don't agree your expressions for M(x). In each case one of the terms is not right. The definition of a moment is force times PERPENDICULAR distance. Look at it again. The moment at a section is the algebraic sum of moments on one side of that section. So it can always be checked by looking at the other side of the section; you should then get the same result.

 

[Dell]

There are 3 contributions to the deflection at B. Can you identify them? .

1) the deflectin of DC,
2) the spread force q
3)the axial force and deflection of AB?

if this is so, how do i find it?? the area of AB is not given

 

[pongo38]

Let's say that C moves to C' as a result of the axial extension of DC. Where is C' in relation to C? Try sketching the exaggerated shape of the deflection as accurately as you can. Your remark that you don't know the area A is also true of EI for the beam. So I assume you are just developing a formula as an answer. CB is a cantilever extension to a beam. What is the difference between that and a cantilever built into a wall rigidly? I think you will find Mohr's theorems for slope and deflection applicable to this problem. Does that help?