[Help] in the integration of electric field

[bibo_dvd]

Hello guys ! :)

i need your help in the integration which is used to calculate the total charge in the electric field

in a continuous volume charge distribution

in this example i can't understand how the integration was done ..so please help me with this :)

The example :

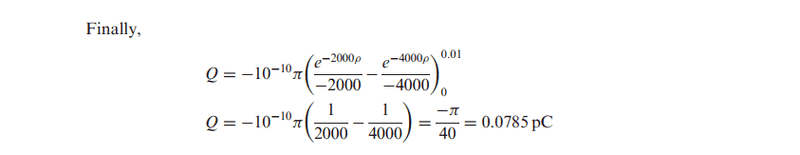
iam not very good in integration so i need your help ...Thanks guys !

 

[SteamKing]

What, specifically, are you having trouble with? If you are not very good at integration, then you need to review the subject and work some practice problems.

 

[bibo_dvd]

the problem is that iam not very good at integration :( and i don't know from where should i start ..i mean which book or tutorial should i start with to help me with this type of examples ?? :)

 

[jim hardy]

Looks to me like there's a mistake in the textbook
Blue figure gives charge as so many microcoulombs per cubic meter

and text below gives it as same number of microcoulombs per square meter.

So it's just a triple integration to get volume, but you integrate wrt z last because ρ is a f(z).

I'd solve it for volume first with ρ a constant(1?), to gain confidence in my ability to triple integrate.
Then go back and include the p(z) in the third intergral.

At least I think that's what i would do ... It's been decades.


Might be you need to go back to your calculus book. It is important to work so many problems they become second nature.

old jim

old jim

 

[alphy]

Hello there,

I would be happy to help you with understanding the integration used to calculate the total charge in an electric field. Integration is a mathematical technique used to calculate the area under a curve. In the context of electric fields, it is used to find the total charge within a continuous volume distribution.

In the example you have provided, the integration is being used to find the total charge within a volume distribution. This is done by breaking up the volume into small elements and calculating the charge within each element. Then, by summing up all the charges in each element, we can find the total charge within the entire volume.

The specific integration technique used in this example may vary depending on the specific problem and distribution of charge. However, the general steps to follow are:

1. Define the volume and the charge density within that volume.
2. Break up the volume into small elements and calculate the charge within each element.
3. Use the integration technique to sum up all the charges in each element.
4. The result of the integration will give you the total charge within the volume.

If you are not familiar with integration, I suggest reviewing the basics first and then applying it to the specific problem you are working on. I hope this helps and good luck!