Help! John Needs to Carry a Long Piece of Wood

[punjabi_monster]

calculus help :(

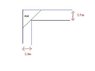
John has to carry a long piece of wood horizontally around the corner from a hallway of width 2 m to a hallway of width 2.5 m. Assuming that the piece of wood has no width, what is the maximum length of this piece of wood (in meters)? Give answer to two decimal places.

i do not get htis question. any help would be greatly appreciated.

the way i tried it was to just use pythagorums theorum and i got 3.20, but i dotn think that's right.

 

[Dr.Brain]

Imagine a L-shaped passage which changes its width while turning from a width of 2m to a width of 2.5 m and you are carrying the piece of wood horizontally , so when you turn, you will face problem if your piece of wood is too long . Calculate the length needed at critical turning point.

BJ

 

[siddharth]

Imagine a L-shaped passage which changes its width while turning from a width of 2m to a width of 2.5 m and you are carrying the piece of wood horizontally , so when you turn, you will face problem if your piece of wood is too long . Calculate the length needed at critical turning point.

BJ

But what if it is carried this way? (Refer picture)
In this case, let the angle the rod make with the horizontal be "theta".
Find the length of each part of the rod in term's of theta. Now the sum of the length of each part is constant. So use calculus and find the maximum value

 

[HallsofIvy]

But what if it is carried this way? (Refer picture)
In this case, let the angle the rod make with the horizontal be "theta".
Find the length of each part of the rod in term's of theta. Now the sum of the length of each part is constant. So use calculus and find the maximum value

I think that's exactly what Dr. Brain was saying! (Your "horizontal" is different from his!)

 

[saltydog]

Punjabi, you following this? I've attached a graph, drawn to scale. Note where theta is. Can you calculate the length of the ladder (or wood or whatever) across both hallways as a function of theta? The ladder will just fit around the corner when this function reaches a minimum. You can calculate that right? What is the ladder length as a function of theta? Break it up into two parts, h and k, as functions of theta.

 

[punjabi_monster]

so...

you are trying to max x +y

sinθ=2.5/y
y=2.5/sinθ

cosθ=2/x
x=2/cosθ

2.5/sinθ + 2/cosθ = sum

from this part i get confused...

2.5/cosθ - 2/sinθ = ds/dt
2.5/cosθ - 2/sinθ = 0
2.5/cosθ = 2/sinθ

the answer is 6.35.

 

[OlderDan]

so...

you are trying to max x +y

sinθ=2.5/y
y=2.5/sinθ

cosθ=2/x
x=2/cosθ

2.5/sinθ + 2/cosθ = sum

from this part i get confused...

2.5/cosθ - 2/sinθ = ds/dt
2.5/cosθ - 2/sinθ = 0
2.5/cosθ = 2/sinθ

the answer is 6.35.

Your derivative is wrong. Those trig functions are in the denominators of those fractions.

\frac{dsin\theta}{d\theta} = cos\theta \ ,\ \ but \ \ \ \frac{d}{d\theta}\left[\frac{1}{sin\theta}\right] \ne \frac{1}{cos\theta}

 

[punjabi_monster]

then would it be:
2.5cscθ + 2secθ = y
2.5(-cscθ)(cotθ)(dθ/dt) + 2(secθ)(tanθ)(dθ/dt) = y'
2.5(-cscθ)(cotθ)(dθ/dt) + 2(secθ)(tanθ)(dθ/dt) = 0

and what would u do next? i am confused.

 

[HallsofIvy]

Where did t come from? To find the θ that maximizes the length, differentiate with respect to θ:

-2.5 (cscθ)(&cotθ)+ 2(secθ)(tanθ)= 0.

You should be able to 2.5 cos³θ+ 2sin³= 0.

 

[punjabi_monster]

ok thanks for your help...i managed to get the right answer.