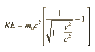Help me find my error in a relativistic kinetic energy calculation

[Serenityseeker22]

Hi everyone.
Given: an asteroid with the mass of 50,000,000 kg, which is moving with the velocity of oh-my-god particle -- 99.99999999999999999999951% of c.
Due to relativistic effects, its total kinetic energy will be 1.44 E+36 Joules (Lorentz factor = 3.2 E+11).
A hypothetical particle accelerator accelerates bodies 40,000,000 times faster than the most powerful real accelerator.
The energy needed to accelerate such asteroid to this speed is several orders of magnitude lower than the total kinetic energy, or around 4.5 E+24 Joules
I know that there's some mistake, but can't see it yet.

 

[jtbell]

We can't see your mistake either, unless you show us the details of your calculations.

 

[Serenityseeker22]

What I'm trying to say is that the energy needed to accelerate the asteroid is much lesser, than the total kinetic energy this asteroid distributes. It violates some laws of physics, I'm sure of it, but I don't know what exactly and how.

My calculations:

Lorentz factor --

oh-my-god particle's speed -- 99.99999999999999999999951% of light speed
light speed -- 299,792,458 m/s
Relativistic kinetic energy --

mass -- 50,000,000 kg
Lorentz factor calculation

v² / c² = (0.9999999999999999999999951 * 299,792,458)² / 299,792,458 ² = 0,9999999999999999999999902

Thus, Lorentz factor equals -- 1 / √(1-0,9999999999999999999999902 ) = 319 438 282 499,97

Total kinetic energy equals 50,000,000 * 299,792,458²*(319 438 282 499,97-1), or rougly 1.435 E+36 Joules

To accelerate an asteroid to such speed, I used the same formula sans the Lorentz factor. So, energy needed to accelerate this rock by a hypothetical particle accelerator is 4.5 E+24 Joules
Where's my mistake?

 

[jbriggs444]

I used the same formula sans the Lorentz factor.

What same formula? Show your work. And why ever would you remove the Lorentz factor?

 

[Nugatory]

To accelerate an asteroid to such speed, I used the same formula sans the Lorentz factor. So, energy needed to accelerate this rock by a hypothetical particle accelerator is 4.5 E+24 Joules

Where did that $4.5\times{10}^{24}$ number come from? How did you calculate it? Show your work.

You can simplify the calculations some by setting $c=1$ to get rid of the factors of 299792458. This is equivalent to choosing to measure distances in units of light-seconds instead of meters (the speed of light is one light-second per second) so doesn't change the physics. You can always convert back to Joules when you're done.

Don't use a hand calculator for problems like this one. You have so many decimal places in some of your numbers that roundoff errors will kill your accuracy. Instead, you can use one of the many online arbitrary precision calculators - google for "online infinite precision calculator".

 

[Serenityseeker22]

Where did that $4.5\times{10}^{24}$ number come from? How did you calculate it? Show your work.

You can simplify the calculations some by setting $c=1$ to get rid of the factors of 299792458. This is equivalent to choosing to measure distances in units of light-seconds instead of meters (the speed of light is one light-second per second) so doesn't change the physics. You can always convert back to Joules when you're done.

Don't use a hand calculator for problems like this one. You have so many decimal places in some of your numbers that roundoff errors will kill your accuracy. Instead, you can use one of the many online arbitrary precision calculators - google for "online infinite precision calculator".

Same formula,KE=M*C² just without Lorentz factor, because I thought it's only relevant when the body moves with relativistic speeds, not when it gets accelerated. Of course I might be wrong, and I probably am, that's why I'm asking.

 

[Dale]

when the body moves with relativistic speeds, not when it gets accelerated.

As you accelerate to relativistic speed the body moves with relativistic speed. You need the Lorentz factor.

 

[Serenityseeker22]

As you accelerate to relativistic speed the body moves with relativistic speed. You need the Lorentz factor.

That's what I needed to hear, thank you very much.

 

[jbriggs444]

KE=M*C2

KE=MC^2 never tells you kinetic energy. It always tells you rest energy.

 

[Khashishi]

Of course, the kinetic energy is equal to the energy it takes to accelerate the mass from rest.