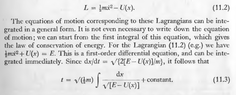Help me solve this integral for the equation of motion

[gionole]

Homework Statement

...

Relevant Equations

...

We have $U(x) = U(a) + \frac{1}{2}U''(a)(x-a)^2$ (by taylor series)

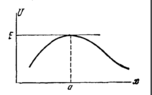
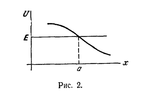
It's known that $U'(a) = 0$ and point $a$ is a turning point, hence at that point, Kinetic energy is 0, and $E = U(a)$, hence:
We have $U(x) = E + \frac{1}{2}U''(a)(x-a)^2$I need to get equation of motion and I want to use the following.
$t = \sqrt{\frac{1}{2}m} \int \frac{dx}{E - U(x)}$
$t = \sqrt{\frac{1}{2}m} \int \frac{dx}{E - E - \frac{1}{2}U''(a)(x-a)^2}$
$t = \sqrt{\frac{1}{2}m} \int \frac{dx}{ - \frac{1}{2}U''(a)(x-a)^2}$

I couldn't solve this. The book proceeds to mention that solution is:

$x(t) = a + se^{\pm \lambda t}$ where $s = x(0) - a$ and $\lambda^2 = -\frac{U''(a)}{m}$

Attaching the image.

 

[kuruman]

This equation $t = \sqrt{\frac{1}{2}m} \int \frac{dx}{E - U(x)}$ is dimensionally incorrect. How did you get and what does it mean? Are you looking for a specific time between two points or are you looking for an expression for $t$ as a function of $x?$ Note that you have a harmonic oscillator potential here and you know very well what $x(t)$ is.

 

[gionole]

No, it's not incorrect. Attaching the image to help you see.

 

[TSny]

Note the square root in the denominator.

 

[gionole]

Ah, I'm sorry. So I get to:

$t = \sqrt{\frac{1}{2}m} \int \frac{dx}{\sqrt{ - \frac{1}{2}U''(a)(x-a)^2}}$

$t = \frac{\sqrt{\frac{1}{2}m}}{\sqrt{\frac{1}{2}}} \int \frac{dx}{\sqrt{ -U''(a)(x-a)^2}}$
$t = \frac{\sqrt{m}}{\sqrt{ -U''(a)}} \int \frac{dx}{x-a}$
$t = \sqrt{-\frac{m}{U''(a)}} \int \frac{dx}{x-a}$
$t = \sqrt{-\frac{m}{U''(a)}} ln(|x-a|) + c$

hm, I think I can arrive after that.

 

[vanhees71]

This is a somewhat overcomplicated way to solve for the harmonic oscillator. Nevertheless it's worth the effort, because the method is also applicable in more complicated cases. Of course, the equation is derived from momentum conservation, which is a first integral of the equations of motion,
$$E=\frac{m}{2} \dot{x}^2+\frac{m}{2} \omega^2 x^2, \quad m \omega^2=V''(a),$$
and I've assumed that we shifted our coordinate system such that $a=0$.

Now you can solve for $\dot{x}$:
$$\dot{x} = \pm \sqrt{\frac{2E}{m} -\omega^2 x^2}.$$
Now comes the quibble with this method, i.e., you have to carefully define what you mean by the square root and the sign ambiguity. To that end we note that the equation implies that $2E/m-\omega^2 x^2 \geq 0$, i.e., we can write $2E/m=\omega^2 x_m^2$ and
$$\dot{x}=\pm \omega \sqrt{x_m^2-x^2}.$$
Now we can understand the motion qualitatively. We always start with some initial condition $x(0)=x_0$, $\dot{x}_0=v_0$. Then we get
$$E=\frac{m}{2} v_0^2 + \frac{m \omega^2}{2} x_0^2,$$
and the above rewriting of $\dot{x}$ is justified.

Now it's clear what happens. Initially the formula (*) with the sign defined by the sign of $v_0$ is valid, and $-x_m \leq x_0 \leq +x_m$. Now the particle moves (according to the sign to the left or the right starting from $x_0$) until it hits the corresponding boundary of the energetically allowed region, i.e., $x$ gets $x_m$ or $-x_m$. At this point also $\dot{x}=0$, and from now on you have to use the other sign (*) to integrate furter, until $x$ reaches the other boundary $-x_m$ or $+x_m$, and so on. It's clear that the motion is periodic with the period given by Eq. (*).

Now we can solve the problem using this equation by separation of variables,
$$\mathrm{d} t = \pm \mathrm{d} x \frac{1}{\omega \sqrt{x_m^2-x^2}}.$$
For definiteness let's assume that at $t=0$ the upper sign is valid, i.e., $v_0>0$ and $-x_m<x_0<x_m$. So for not too large times we can stick with the upper sign:
$$t=\int_0^t \mathrm{d} t' =\frac{1}{\omega x_m} \int_{x_0}^x \mathrm{d} x' \frac{1}{\sqrt{1-(x'/xm)^2}}=\frac{1}{\omega} [\arcsin(x/x_m)-\arcsin (x_0/x_m)]$$
or
$$x(t)=x_m \sin(\omega t+\varphi_0), \quad \varphi_0=\arcsin(x_0/x_m).$$
Now you can determine $x_m$ and $\varphi_0$ by again using the initial conditions. You can now show that this already is the full solution for all $t>t_0$ by directly checking that it solves the equation of motion.

Of course it's much easier to simply solve the equation of motion,
$$\ddot{x}=-\omega^2 x,$$
whose general solution is easily shown to be
$$x(t)=A \cos(\omega t) + B \sin(\omega t),$$
with $A$ and $B$ being determined uniquely by the inital conditions, and this can of course also brought into the form we derived by the above somewhat more complicated method, using the energy conservation integral.

 

[kuruman]

It's known that U′(a)=0 and point a is a turning point, hence at that point, Kinetic energy is 0, and E=U(a), hence:

That is not true, $a$ is not a turning point. It is the point at which the potential energy function has a minimum, also known as the equilibrium point. At that point, the first derivative of the potential energy, i.e. the force on the mass, vanishes as you noted. The turning points are equidistant from $a$ at $x=a \pm x _0.$ You need to rethink this.

 

[vanhees71]

I also forgot to say, you understand all my long arguments much easier when drawing $V$ as function of $x$ and a horizontal line at $V=E$...

 

[gionole]

Why do you all say $a$ is not turning point ? attaching the image of the problem now. you can see E at $a$ is equal to $U$. This is only when Kinetic energy is 0 and that can only be true when speed is 0, hence turning point.

Also problem says: "
Determine approximately the law of motion of the particle in the field U(x) near the stopping point x==a"

 

[kuruman]

Why do you all say $a$ is not turning point ?

Because the force on the particle at $x=a$ is $F=-U'(a)=0$. If its kinetic energy is zero at that point and the force on it is also zero, why should its position change?

 

[gionole]

1. True but when book says $a$ is a stopping point, that definitely means speed is 0, hence $K = 0$, hence $E = U(a)$. Where am I wrong here ?
2. force is 0, agreed. but K = 0 as well. now I don't know why position would change. Wouldn't potential energy field change its position ? i mean we say potential energy is not 0, but force is 0. What does that mean then ? particle won't move ? then what does non-zero potential energy do to the particle ? nothing ?

By using the notion I said, K=0, E = U(a), I now arrive at the correct answer. if you're correct, then how would I arrive at the correct answer ?
$t = \sqrt{\frac{1}{2}m} \int \frac{dx}{\sqrt{ - \frac{1}{2}U''(a)(x-a)^2}}$

$t = \frac{\sqrt{\frac{1}{2}m}}{\sqrt{\frac{1}{2}}} \int \frac{dx}{\sqrt{ -U''(a)(x-a)^2}}$
$t = \frac{\sqrt{m}}{\sqrt{ -U''(a)}} \int \frac{dx}{x-a}$
$t = \sqrt{-\frac{m}{U''(a)}} \int \frac{dx}{x-a}$
$t = \sqrt{-\frac{m}{U''(a)}} ln(|x-a|) + c$

 

[kuruman]

True but when it says it's a stopping point,

What is "it" and where does "it" say that it is a stopping point? I cannot read the Cyrillic text where $a$ is introduced.

 

[gionole]

What is "it" and where does "it" say that it is a stopping point? I cannot read the Cyrillic text where $a$ is introduced.

I copy this from the book:

Определить приближенно закон движения части-цы в поле U(х) вблизи точки остановки х==а (рис. 2).
Указание. Воспользоваться разложением U(х) в ряд Тейлора вблизи точки х=а. Рассмотреть случаи U'(a) = 0 и U'(a) !=0, U''(a) !=0

By using translate, we get:

Determine approximately the law of motion of the part in the field U(x) near the stopping point x==a (Fig. 2).
Instruction. Use the expansion of U(x) in a Taylor series near the point x=a. Consider the cases U'(a) = 0 and U'(a) !=0, U''(a) !=0

 

[kuruman]

Does this U'(a) !=0, U''(a) !=0

mean this $U'(a) \neq 0, U''(a) \neq 0~?$

 

[gionole]

Does this U'(a) !=0, U''(a) !=0

mean this $U'(a) \neq 0, U''(a) \neq 0~?$

correct. yes.

 

[kuruman]

Can you post (рис. 2) that the book mentions?

 

[gionole]

Can you post (рис. 2) that the book mentions?

Just so you know, I treat $U'(a) = 0, K = 0, E = U(a)$ and use
$t = \sqrt{\frac{1}{2}m} \int \frac{dx}{\sqrt{ E - U(x)}}$ and I got the correct result that book lists. but now you got me confused that at $x=a$, kinetic energy is 0, force is 0, how would the particle move ? couldn't potential energy cause it to move even if force is 0 ? (note U'(a) = 0, but not U(a))

 

[kuruman]

The confusion is in you not being clear what problem you are solving. Your statement in post #1

It's known that $U′(a)=0$ and point $a$ is a turning point

contradicts the figure that you posted in post #17.

In the figure it is true that point $a$ is a turning point. However $U'(a)$ is not equal to zero as the statement in post #1 claims. If you look at the figure, the slope at $a$ is clearly non-zero.

It is always true that you can write
$U(x)=U(a)+U'(a)(x-a)+\frac{1}{2}U''(a)(x-a)^2.$
You can choose $a$ to be where $U'(a)=0$ OR to be a turning point where $U(a)=E$. If you want to have both conditions satisfied, the particle must be at rest at point $a$ as we have already seen.

So what problem are you trying to solve?

 

[gionole]

The confusion is in you not being clear what problem you are solving. Your statement in post #1

contradicts the figure that you posted in post #17.

In the figure it is true that point $a$ is a turning point. However $U'(a)$ is not equal to zero as the statement in post #1 claims. If you look at the figure, the slope at $a$ is clearly non-zero.

It is always true that you can write
$U(x)=U(a)+U'(a)(x-a)+\frac{1}{2}U''(a)(x-a)^2.$
You can choose $a$ to be where $U'(a)=0$ OR to be a turning point where $U(a)=E$. If you want to have both conditions satisfied, the particle must be at rest at point $a$ as we have already seen.

So what problem are you trying to solve?

Thanks for the analysis. everything clear now to be honest. It has to be at rest. Thanks so much

 

[vanhees71]

Why do you all say $a$ is not turning point ? attaching the image of the problem now. you can see E at $a$ is equal to $U$. This is only when Kinetic energy is 0 and that can only be true when speed is 0, hence turning point.

Also problem says: "
Determine approximately the law of motion of the particle in the field U(x) near the stopping point x==a"

No, your $a$ is a stable (local) equilibrium point, i.e., a minimum of the potential. The turning points are the points, I've calculated in #6. Just draw the potential as function of $x$ and a line $V=E=\text{const}$. Then it's very easy to see!