ChaosTheory
- 4
- 0
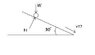
I was wondering if anyone could help me out with this problem. Using the drawing attached, I have to find the velocity of the ball at the end of the incline, where the ball starts from rest. This isn't the whole problem, but this is what is giving the entire class (M.E. Dynamics) a major headache. Our professor can't even solve it. We keep finding more variables than equations. If possible, do it without DiffEqu.
Also, if you're interested, this problem is part of the project in R.C. Hibbeler's Engineering Mechanics: Dynamics (10th ed.) on page 94.
I appreciate any help you can give me.
Thanks,
Mike
Also, if you're interested, this problem is part of the project in R.C. Hibbeler's Engineering Mechanics: Dynamics (10th ed.) on page 94.
I appreciate any help you can give me.
Thanks,
Mike