Help Needed: Resolving a Vertical Force into Components

[Oblivion77]

Hey guys, I am stuck on this question. I was wondering if anyone can help me. I am going to attach a picture.

Here is the question.



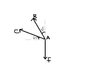
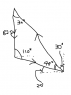
The magnitude of the vertical force F is 82.5 N. If you resolve it into components Fab and Fac. What are the magnitudes of these components? (unit: Newtons, N, for both parts)

Thanks!

 

[tiny-tim]

Welcome to PF!

The magnitude of the vertical force F is 82.5 N. If you resolve it into components Fab and Fac. What are the magnitudes of these components? (unit: Newtons, N, for both parts)

Hi Oblivion77! Welcome to PF!

Can you describe the picture (it will take hours to get approval for it)?

And show us what you've tried, and where you're stuck, and then we'll know how to help you.

 

[Oblivion77]

Sorry, here is the pic.

 

[HallsofIvy]

That was not his point. It is much easier to read if you simply describe the vectors, giving lengths and angles rather than either attaching pictures or giving links to other sites.

Here, F is pointing straight down and you told us it has "length" 82.5 N. AB points up to the left at 30 degrees to the vertical. AC points up to the left also but at 20 degrees to the horizontal. Extend AB back down to the lower right and drop a perpendicular from the tip of F to that line. You now have a right triangle with hypotenuse of length 82.5 and angle 30 degrees at A ("vertical angles are congruent"). The projection of F on that (the "near side") is 82.5 cos(30). Do the same with AC.

 

[Oblivion77]

I don't understand what you mean "Extend AB back down to the lower right and drop a perpendicular from the tip of F to that line" We haven't learned anything about "perpendiculars" yet.

 

[tiny-tim]

The magnitude of the vertical force F is 82.5 N. If you resolve it into components Fab and Fac. What are the magnitudes of these components?

Hi Oblivion77!

Having seen the picture, I don't really understand the question.

"resolve into components" (in the plural) usually refers to components in perpendicular directions (like x and y).

Does the question actually say that, or does it just say what are the components of F (i) along ab (ii) along ac?

Or is this part of a force diagram for a bigger problem?

Anyway, what formula has your teacher given you for finding a component? ​

 

[Oblivion77]

Hi Oblivion77!

Having seen the picture, I don't really understand the question.

"resolve into components" (in the plural) usually refers to components in perpendicular directions (like x and y).

Does the question actually say that, or does it just say what are the components of F (i) along ab (ii) along ac?

Or is this part of a force diagram for a bigger problem?

Anyway, what formula has your teacher given you for finding a component? ​

Here is the original picture, since it doesn't have vectors yet I think "resolve into components" means to make it into vectors. Here it is.

 

[tiny-tim]

Here is the original picture, since it doesn't have vectors yet I think "resolve into components" means to make it into vectors. Here it is.

hmm … I think the question is very badly written …

I think it means simply
(i) what is the component of F along AB?
(ii) what is the component of F along AC?

(usually with a diagram like that, it would ask what are the tension forces in AB and AC, but it's clearly not doing that)

And of course you find that just by multiplying by cos of the appropriate angle (and be careful about the ± sign).

 

[Oblivion77]

So How could I solve this question by drawing it out?

 

[ephedyn]

============================ Edit: disregard this, I got it wrong, it's not in equilibrium ============================
There are two useful tools to solving this. Since it's a system in equilibrium, consider

1) drawing a closed polygon
2) the coincidence of the lines of action

I'd have done (1), and I didn't read through his solution but I'm betting HallsofIvy got it for you.
============================ Edit: disregard this, I got it wrong, it's not in equilibrium ============================

 

[Oblivion77]

There are two useful tools to solving this. Since it's a system in equilibrium, consider

1) drawing a closed polygon
2) the coincidence of the lines of action

I'd have done (1), and I didn't read through his solution but I'm betting HallsofIvy got it for you.

I don't really understand what HallsofIvy is saying, is he saying make a triangle by drawing a line from the tip of F to B?

 

[Oblivion77]

Edit

 

[ephedyn]

============================ Edit: disregard this, I got it wrong, it's not in equilibrium ============================

Argh, I'm guessing HallsofIvy is a mathematician by making. How about my drawing ^_^?

Edit: No wait, I realized a directional problem on one of the vectors... let me see...

============================ Edit: disregard this, I got it wrong, it's not in equilibrium ============================

 

[ephedyn]

OK, I'm back. Sorry, it's not in equilibrium. But what HallsofIvy described was still correct.

 

[Oblivion77]

OK, I'm back. Sorry, it's not in equilibrium. But what HallsofIvy described was still correct.

Yeah I figured that out from hallsofivy, so I got 82.5Cos30 and 82.5Cos20, i found out the values of those. But they are incorrect. Am I missing something?

 

[ephedyn]

Scribbling things in paint is clearly not my strength, disregard the 60 deg, it should read 90 deg, thereby 90-20=70 for the angle between the line of action of the force and the hinged lever. Are you certain it's not

|Fab| = 82.5 cos 30

|Fac| = 82.5 cos 70

in degrees?

 

[tiny-tim]

cosine rule

So How could I solve this question by drawing it out?

HallsofIvy was just talking about the cosine rule.

Do you know the cosine rule (or any rule) for finding a component?