Help,this problem cost me much time

[goodboy]

How to get this conclusion

if we know the magnetic moment m,and the magnetic induction B.then the force is

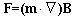
who can tell me how to get this.thanks very much

 

[quasar987]

Hopefully you know that for a current loop of steady current in a uniform magnetic field, the mechanical energy of interaction is $U_{mech}= -m\cdot B$, making the force on the loop $\vec{F}=\nabla(m\cdot B)$. Now use the vector identity that says

$$\nabla (m\cdot B) = m\times (\nabla \times B) + B \times (\nabla \times m)+(m\cdot \nabla)B+(B\cdot \nabla)m$$

The first term vanishes because $\nabla \times B=0$ in the absence of current or changing electric fields. m taken as a vector field is constant wrt change in position, so all its derivative wrt position are null, making the 2nd and 4th term vanish. Remains the 3rd term