- #1
jisbon
- 476
- 30
- Homework Statement
- NIL
- Relevant Equations
- NIL
Hello all!
Thanks for helping me out so far :) Really appreciate it.
I don't seem to understand some of the questions presented to me, so if anyone has an idea on how to start the questions, please do render your assistance :)
4)
Take ##3+7i## is a solution of ##3x^2+Ax+B=0##
Since ##3+7i## is a solution, I can only gather :
##(z−(3+7i))(...)=3x2+Ax+B##
Not sure on how to go from here.
EDIT: I got A =18 and B=174, is this correct?
I recognized that since there's a 3, this means the other root must be a conjugate, hence
##(z-(3+7i))(z-(3-7i))##
##(z-3)^2-(7i)^2 =0##
##z^2+6z+58=0##
##3z^2+18z+174=0##
6)
Suppose ##z=2e^{ikπ}##and
##z^{n}=2^5 e^{iπ/8}##
Find k such that z has smallest positive argument
I don't understand this question :/ For z to have smallest positive principal argument, what does it entail/mean?
EDIT: Tried again. Got the following:
##z^{n}=2^n e^{inkπ} = 2^5 e^{iπ/8}##
## nk = 1/8##
##5k =1/8##
##k = 1/40##?7)
Let
##\sum_{k=0}^9 x^k = 0##
Find smallest positive argument. Same thing as previous question, but I guess I can expand to
z+z2+z3+...+z9=0z+z2+z3+...+z9=0
##z=re^iθ##
##rei^θ+re^2iθ+re^3iθ+...##
What do I do to proceed on?
Cheers
Thanks for helping me out so far :) Really appreciate it.
I don't seem to understand some of the questions presented to me, so if anyone has an idea on how to start the questions, please do render your assistance :)
1)
Suppose
(a+bi)(c+di)(e+fi)=4+8i(a+bi)(c+di)(e+fi)=4+8i
Find the value of
(a2+b2)(c2+d2)(e2+f2)(a2+b2)(c2+d2)(e2+f2)
Not sure what I'm suppose to do here, expanding is probably out of the question, does squaring (a+bi)(c+di)(e+fi)(a+bi)(c+di)(e+fi) helps to find out (a2+b2)(c2+d2)(e2+f2)(a2+b2)(c2+d2)(e2+f2)?
2)
Let
S=(cos(π/5)+isin(π/5))n,nϵNS=(cos(π/5)+isin(π/5))n,nϵN
What I understand here is that I'm supposed to find the amount of distinct roots in this equation? How do I even start?
5)
Let ∣z1∣=∣z2∣=7∣z1∣=∣z2∣=7
If ∣z1+z2∣=2∣z1+z2∣=2,solve ∣1/z1+1/z2∣
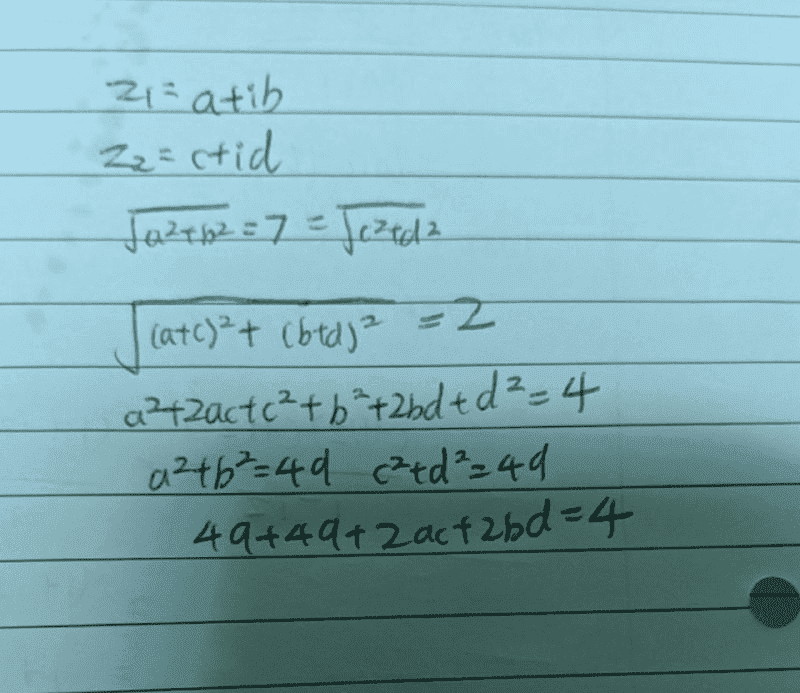
How do I even proceed from here?
3)
Let z be complex number that allows:
z+7¯¯¯z=∣¯¯¯z+4∣∣z+7z¯=∣z¯+4∣
Find z.
My working:
a+bi+7(a−bi)=∣(a+4)+bi∣a+bi+7(a−bi)=∣(a+4)+bi∣
8a−6bi=√(a+4)2+b28a−6bi=√(a+4)2+b2
64a2−96abi−36b2=a2+8a+16+b264a2−96abi−36b2=a2+8a+16+b2
Not sure where to proceed from here.
Suppose
(a+bi)(c+di)(e+fi)=4+8i(a+bi)(c+di)(e+fi)=4+8i
Find the value of
(a2+b2)(c2+d2)(e2+f2)(a2+b2)(c2+d2)(e2+f2)
Not sure what I'm suppose to do here, expanding is probably out of the question, does squaring (a+bi)(c+di)(e+fi)(a+bi)(c+di)(e+fi) helps to find out (a2+b2)(c2+d2)(e2+f2)(a2+b2)(c2+d2)(e2+f2)?
2)
Let
S=(cos(π/5)+isin(π/5))n,nϵNS=(cos(π/5)+isin(π/5))n,nϵN
What I understand here is that I'm supposed to find the amount of distinct roots in this equation? How do I even start?
5)
Let ∣z1∣=∣z2∣=7∣z1∣=∣z2∣=7
If ∣z1+z2∣=2∣z1+z2∣=2,solve ∣1/z1+1/z2∣
How do I even proceed from here?
3)
Let z be complex number that allows:
z+7¯¯¯z=∣¯¯¯z+4∣∣z+7z¯=∣z¯+4∣
Find z.
My working:
a+bi+7(a−bi)=∣(a+4)+bi∣a+bi+7(a−bi)=∣(a+4)+bi∣
8a−6bi=√(a+4)2+b28a−6bi=√(a+4)2+b2
64a2−96abi−36b2=a2+8a+16+b264a2−96abi−36b2=a2+8a+16+b2
Not sure where to proceed from here.
Take ##3+7i## is a solution of ##3x^2+Ax+B=0##
Since ##3+7i## is a solution, I can only gather :
##(z−(3+7i))(...)=3x2+Ax+B##
Not sure on how to go from here.
EDIT: I got A =18 and B=174, is this correct?
I recognized that since there's a 3, this means the other root must be a conjugate, hence
##(z-(3+7i))(z-(3-7i))##
##(z-3)^2-(7i)^2 =0##
##z^2+6z+58=0##
##3z^2+18z+174=0##
6)
Suppose ##z=2e^{ikπ}##and
##z^{n}=2^5 e^{iπ/8}##
Find k such that z has smallest positive argument
I don't understand this question :/ For z to have smallest positive principal argument, what does it entail/mean?
EDIT: Tried again. Got the following:
##z^{n}=2^n e^{inkπ} = 2^5 e^{iπ/8}##
## nk = 1/8##
##5k =1/8##
##k = 1/40##?7)
Let
##\sum_{k=0}^9 x^k = 0##
Find smallest positive argument. Same thing as previous question, but I guess I can expand to
z+z2+z3+...+z9=0z+z2+z3+...+z9=0
##z=re^iθ##
##rei^θ+re^2iθ+re^3iθ+...##
What do I do to proceed on?
Cheers
Last edited: