Torshi
- 118
- 0
Homework Statement
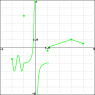
See attachment: what is the interval notation of the continuous line
Homework Equations
no equation
The Attempt at a Solution
(-2,-1)U(-1,inf) ? not sure then it goes to 1 then to -inf? There are two continuous lines
(-2,-1)U(-1,1)U(1,inf)? No...
i feel like an idiot on this problem
Attachments
Last edited: