senseandsanity
- 10
- 0
I need help with this question (the picture is attached):
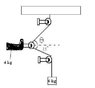
A foot, mass of 4 kg, is suspended by a pulley system. The net traction force needs to pull straight out on the leg. What is the proper angle theta for the upper rope?
I know that the system is frictionless so the tension in the entire rope is the force due to gravity (6 kg*9.81m/s^2) but I'm not sure what to do next.
A foot, mass of 4 kg, is suspended by a pulley system. The net traction force needs to pull straight out on the leg. What is the proper angle theta for the upper rope?
I know that the system is frictionless so the tension in the entire rope is the force due to gravity (6 kg*9.81m/s^2) but I'm not sure what to do next.