Help with Rigid Body Exercise: Determine Speed of B

[Telemachus]

Homework Statement

Hi there, I'm starting with rigid body, and I'm having some trouble with it, so I'll need your help :D

I have this exercise now, but I will probably come with some others later.

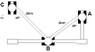
The exercise says: The collars A and C glide along the vertical rods and B of the horizontal. If C has a downward speed of 0.2m/seg. when it reaches plotted to determine the angular velocity of the rod AB.

So, what I think I have to do at first, is to determine the speed of B. Is this right? so I've proceeded this way:

$$V_c=V_{cm}+\omega\times{R_{c/q}}$$

$$R_{c/q}=25\cos45º \hat{i}+25\sin45º \hat{j}$$

With this I would find the omega between B and C, and then the speed of B.
$$V_B=V_{cm}+\omega\times{R_{b/q}}$$

What you say?

Bye there and thanks for your help :)

PD: Sorry for the pic. The vertical rods are larger :P

 

[tiny-tim]

Hi Telemachus!

(a bit late, I know, but perhaps this will help)

So, what I think I have to do at first, is to determine the speed of B. Is this right? so I've proceeded this way*…

No, I wouldn't do it that way at all.

You're treating this as a physics problem, with centre of mass etc.

It isn't, it's purely a geometry problem …

call the two angles θ and φ, and find the geometric relation between them.

Then differentiate that to get dφ/dθ

 

[Telemachus]

Thanks tiny!