wikidrox
- 44
- 0
I can't quite get an answer for these damn questions. It feels like there is information missing.
1. Show that the minimum stopping distance for a car traveling at speed v is equal to v^2 / 2*coefficient of friction*g, where the coefficient of static friction is between tires and the road and g is acceleration due to gravity.
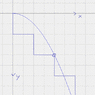
2. A ball rolls off the top of a stairway with a horizontal velocity of magnitude 1.5m/s. The steps are 20 cm high and 20 cm wide. Which step will the ball hit first?
1. Show that the minimum stopping distance for a car traveling at speed v is equal to v^2 / 2*coefficient of friction*g, where the coefficient of static friction is between tires and the road and g is acceleration due to gravity.
2. A ball rolls off the top of a stairway with a horizontal velocity of magnitude 1.5m/s. The steps are 20 cm high and 20 cm wide. Which step will the ball hit first?