Hilbert space transformation under Poincaré translation

[ddd123]

This is one of those "existential doubts" that most likely have a trivial solution which I can't see.

Veltman says in the Diagrammatica book:

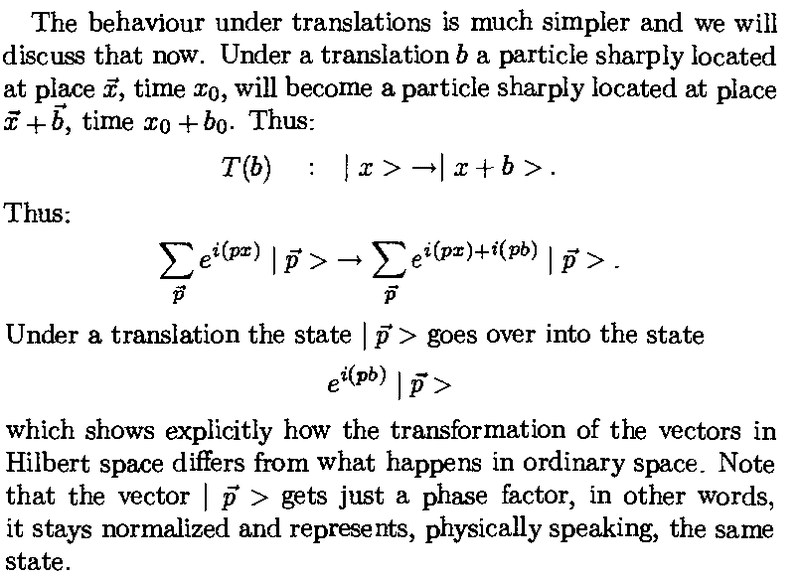
Although the reasoning makes perfect sense for a Hilbert space spanned by momentum states, intuitively it doesn't make sense to me, because a translated particle cannot correspond to the same state "physically speaking" (i.e. the same ray in Hilbert space). How is that possible?

Another question: does this hold for non-relativistic quantum mechanics as well? At a glance, it seems so.

Thanks.

 

[strangerep]

[...]

Although the reasoning makes perfect sense for a Hilbert space spanned by momentum states, intuitively it doesn't make sense to me, because a translated particle cannot correspond to the same state "physically speaking" (i.e. the same ray in Hilbert space). How is that possible?

Well, I can distinguish a particle "here" from a particle "over there". I.e., they don't have to be the same Hilbert space ray. We just want a mapping between them that corresponds to a spatial translation. Moreover, we want a Hilbert space on which all the transformations of the Poincare group are represented by unitary operators. (The terminology is that we want a "unitary irreducible representation" of the Poincare group.)

Another question: does this hold for non-relativistic quantum mechanics as well? At a glance, it seems so.

Yes.
And,... since you needed to ask these questions,... I recommend you grab a copy of Ballentine urgently and study ch3 (and possibly also ch1 and ch2 if ch3 doesn't make sense). He covers this stuff for the nonrel case (Galilei group), but once you understand that properly, the relativistic case will be a bit easier.

 

[ddd123]

Will do. But I've just noticed something. The phase factor is put on the single |p> plane wave component, which by itself is completely delocalized, it's only the superposition of all |p>'s that is localized: so it's ok that the single |p> state is the same. Am I making sense?

 

[strangerep]

Will do. But I've just noticed something. The phase factor is put on the single |p> plane wave component, which by itself is completely delocalized, it's only the superposition of all |p>'s that is localized: so it's ok that the single |p> state is the same. Am I making sense?

Yes -- you're getting your first hint that something more general than Hilbert space is desirable.
That "something" is called "rigged Hilbert space". Ballentine ch1 contains a gentle introduction.