Binki said:
The machine set up was to clear up some initial doubts on the faraday generator/motor effect and was built to completely enclose the magnetic field to eliminate any claims of induction in the external circuit.
I have questions about this that I'll ask later because they are less important to me than others I have.
the field was created by copper coils calculated and tested to give 1.6-1.8 Tesla (16000-18000 Gauss) which was the saturation of the iron we were using.
Very strong magnets.
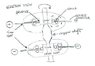
The core was made of two F/disks of 8 inches diameter mounted on a hardened copper shaft with a copper slip ring silver soldered to its perimeter. The disk was part of or centre of the main magnetic keep that enclosed the coils leaving only a 5mm gap through which a copper plate passed in order to extract the current and also a base to hold the coils and brushes.
This I don't understand. The disks were copper. How could they form part of a magnetic circuit? You cannot put a piece of copper across the pole of a horseshoe magnet and form a magnetic circuit. A "keeper" must be of a material in which a magnetic field can be induced by proximity to another magnetic field.
I'm also not understanding the 5mm gap. Perhaps because I'm not sure of the orientation of the electromagnets with regard to the disks. You spoke earlier of a "uniform magnetic field". What that says to me is that on one side of the copper disks you have a north pole pointed at the disks which completely covers the whole area of that side of the disk. On the other side you have a south pole that completely covers the whole area of that side of the disk. There is attraction between the magnets and the magnetic lines of force go directly through the copper disks. Is this how you had it set up?
You can imagine the shape as something like two dinner plates cupped together.
And there was nothing in the space between the "dinner plates, correct?
there were two units on the same shaft in order to double the voltage generated. The brushes were made of 95% silver/carbon (No expense spared) so the no load consumption of the DC motor was only 200 watts approx. Even after all this the machine only produced the calculated 5.6 Volts at 3000 rpm and 3000 Amps approx.
Here, now, is something I find very problematic. 5.6 volts times 3000 amps makes 16,800 watts. You say you're putting roughly 200 watts into the driving motor, and so the rest must be going into the electromagnets. The trouble is that since it is a static magnetic field there is no reason you couldn't replace the electromagnets with permanent magnets of the same strength and apparently harvest the same 16,800 watts with only a 200 watt imput.
I understand this wasn't the focus of your experiment, but you can see that you are proposing something that inadvertantly becomes a case for "Free Energy".
One of the fascinating features of this set-up was to see the motor side turn at any speed (from almost standstill to the equivalent speed of the generator) adjusted by the field strength, with a torque equivalent to the Watts involved. That is even at 1 rpm the turning power was there you could hold on to the shaft and it was humanly impossible to stop by hand.
What do you mean "the motor side"? Thus far, all you have mentioned is a generator.
If you capture the set-up from my basic explanation you may appreciate that the generated current could have been produced in the core/centre or in the gap through which the copper plate passed in order to extract the current, which of course does not prove or disprove movement of the field.
In view of these other claims about rotating the conductor and magnet together and still generating current, what I need you to make clear is whether or not your electromagnets were fixed to the disks and rotating with them, or whether the conducting disks, alone, rotated.
After all this experiment gave me a very clear view of the concept and did not give any inclination towards OU.
I'm not exactly sure what the concept of OU means or implies, but if the claim is that you're getting more energy out than you had to put in, then your set up seems to have that capability were you to replace the electromagnets with permanent magnets of the same strength. That ought not to be possible, and I don't suppose it is. I hope you can understand the problem I am percieving with getting 16,800 watts out of a device that is essentially only drawing about 200 watts to operate.
The use of coils maybe give an easier comprehension of the field being independent to the source but does not prove rotation or non rotation of the field.
Which brings us back to your other claim about gluing two magnets to a conductor and rotating the whole sandwich together and being able to take current off of it. I think I will try rotating the magnets, one on each side of the conductor, opposite poles, and holding the conductor still. If I get an appreciable amount of current from the conductor it should demonstrate that the magnetic field rotates with the magnets. Does that sound right?