bearhug
- 78
- 0
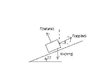
A 100 kg crate is pushed at constant speed up the frictionless 27° ramp shown in the figure. What horizontal force F is required?
What force is exerted by the ramp on the crate?
I can't paste the figure up so I hope this question describes the scenario well enough.
What's giving me problems is how am I suppose to find F when I don't even know n? I figured I use the angle to help solve for others. I know Fg=mg which is (100)(9.8) right? Would that give me one side of the triangle?
What force is exerted by the ramp on the crate?
I can't paste the figure up so I hope this question describes the scenario well enough.
What's giving me problems is how am I suppose to find F when I don't even know n? I figured I use the angle to help solve for others. I know Fg=mg which is (100)(9.8) right? Would that give me one side of the triangle?