putongren
- 124
- 1
Dear All,
How do you derive both equations below. Let r be the position vector (rcos(θ), rsin(θ)), with r and θ depending on time t.
These equations can be found in wiki under polar coordinates.
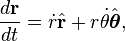
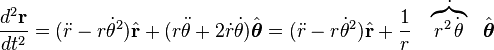
How do you derive both equations below. Let r be the position vector (rcos(θ), rsin(θ)), with r and θ depending on time t.
These equations can be found in wiki under polar coordinates.