Discussion Overview
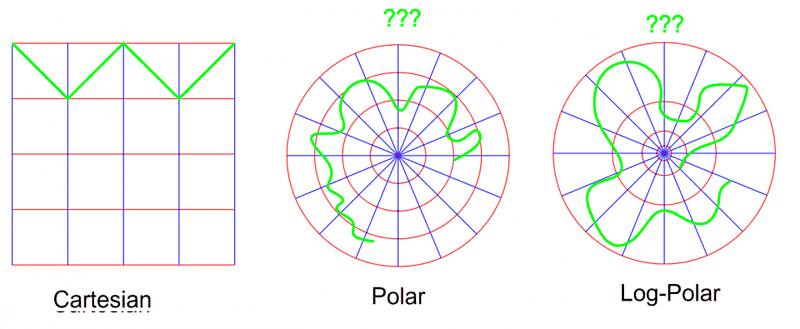
The discussion revolves around the application of conformal mapping to convert curves between different coordinate systems, specifically from Cartesian to polar and log-polar maps. Participants explore the mathematical transformations involved and the challenges associated with expressing functions in these different forms.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant seeks clarification on how to convert a linear function defined in Cartesian coordinates to its equivalent in polar and log-polar coordinates.
- Another participant suggests defining the function properly and transforming the coordinates directly, providing a mathematical expression for the transformation.
- A different participant emphasizes the need to express the relationship in polar coordinates as a function of radius and angle, indicating technical difficulties in doing so.
- One participant discusses the relationship between radius and angle, noting that in logarithmic coordinates, only the radius is affected.
- Another participant argues that functions cannot be expressed in "polar mode," but rather points can be represented in different coordinate systems.
- One participant provides a mathematical derivation for the radius in terms of Cartesian coordinates and discusses potential solutions for expressing the function in polar coordinates.
- A later reply highlights the challenge of expressing a single value of radius for multiple angles, suggesting that paths should be parameterized using a separate parameter.
Areas of Agreement / Disagreement
Participants express differing views on the feasibility of expressing functions in polar coordinates, with some suggesting it is not possible while others propose methods for transformation. The discussion remains unresolved regarding the best approach to achieve the desired conversions.
Contextual Notes
Limitations include the complexity of expressing implicit functions in polar or log-polar coordinates and the potential for multiple radius values corresponding to the same angle.