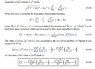How Can Higher Order Relativistic Corrections Improve Hydrogen Atom Models?

[M. next]

For hydrogen atoms, all book take correction up to 1/c^2 where the perturbation is -P^4/8*m^3*c^2. And they go solving it by sandwiching p^4 term where they consider p^2 = 2m*(1+e^2/r). and they square it to solve for p^4.

To get a better view of perturbation to first order please see attachment.


What if I want it to the second order correction, that is to p^6? The additional perturbative term would be p^6/16*m^5*c^4. What should be done in this case?

 

[Einj]

I think you can use the same technique. The only new term you need to evaluate is $\langle n,\ell|\frac{1}{r^3}|n,\ell\rangle$.

 

[M. next]

And what to do with P^6?

 

[Einj]

It's the same technique, you can write:
$$
\frac{p^6}{16m^5c^4}=\frac{1}{2m^2c^4}\left(\frac{p^2}{2m}\right)^3= \frac{1}{2m^2c^4}\left(\frac{p^2}{2m}-\frac{e^2}{r}+\frac{e^2}{r}\right)^3.
$$
You now realize that $\frac{p^2}{2m}-\frac{e^2}{r}=H_0$ and so:
$$
\frac{p^6}{16m^5c^4}=\frac{1}{2m^2c^4}\left(H_0^3+\frac{e^6}{r^3}+3H_0^2\frac{e^2}{r}+3H_0\frac{e^4}{r^2}\right),
$$
and the you exactly what is the eigenvalue for $H_0$.

 

[M. next]

Ohhhh thank you very much!