How Can I Calculate the Frequency of the Left Pendulum in a Coupled System?

[Fabio010]

Coupled physical pendulums (URGENT)

Imagine that you have coupled physical pendulums like this (see image below).

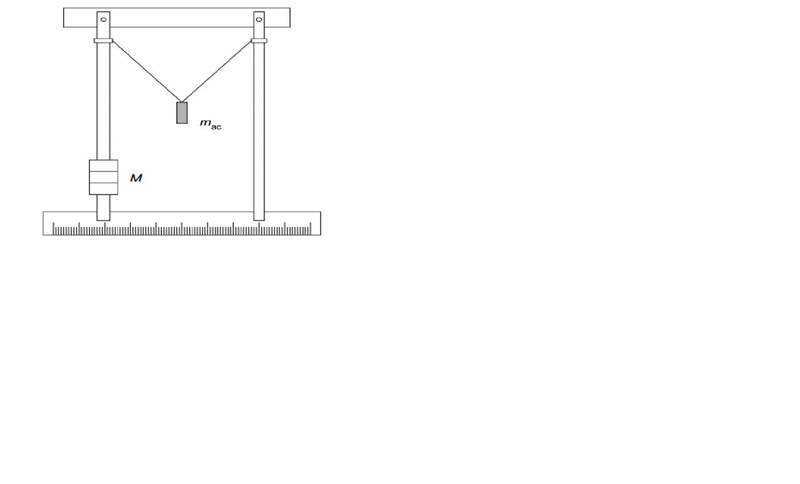
mass is in the inferior part of the pendulum.*

Now we let the right pendulum swing without initial speed = 0 with a certain amplitude. As we know, the amplitude of the right pendulum will decrease , increasing the amplitude of left pendulum.

I have the Period for the max amplitude of the right pendulum. When the amplitude of the right pendulum is zero, i have to mark the max amplitude of the left pendulum.

You can see in the following image:

L it's approximated 1 meter.

d its caused by the coupled pendulums. it's the distance between the equilibrium point without being coupled to the equilibrium point being coupled.

Now how can i calculate the frequency (v max) of the left pendulum??

I just know the period of the right pendulum. I know the max amplitude in left pendulum. How can i calculate the frequency of the left pendulum?

( frequency is induced by right pendulum)? I really need help, its urgent.

 

[Fabio010]

anyone??is something my problem that is not explicit?

 

[AJ Bentley]

anyone??is something my problem that is not explicit?

TBH, I can't make head or tail of it.

 

[Fabio010]

This is all about resonance. When i swing the right pendulum their motions is described as the figure below:

http://www.google.pt/imgres?q=coupled+pendulum&start=143&um=1&hl=pt-PT&sa=N&biw=1097&bih=512&tbm=isch&tbnid=mexJ2ESXZLLxEM:&imgrefurl=http://www.sciencedirect.com/science/article/pii/S0003491611001916&docid=U0f6MP51ZIEygM&imgurl=http://ars.els-cdn.com/content/image/1-s2.0-S0003491611001916-gr1.jpg&w=442&h=236&ei=1gyJUPzAGcaShgfq34HQDg&zoom=1&iact=hc&vpx=384&vpy=243&dur=5467&hovh=164&hovw=307&tx=96&ty=66&sig=108844172008930591831&page=8&tbnh=127&tbnw=238&ndsp=17&ved=1t:429,r:45,s:100,i:139


Knowing the period of the right pendulum, and knowing the max amplitude of the left pendulum, how can i calculate the frequency of the left pendulum? I just need a tip.

 

[AJ Bentley]

The diagram looks like no coupled pendulum arrangement I've ever seen.

You seem to have a rigid bar on the right - which could be a pendulum except that it has no mass associated.
On the left is another bar, this time with a mass so I assume that IS a pendulum. And between them you have a mass suspended on a cord.

The nearest thing to this in standard physics texts is two pendula coupled by a spring. The analysis of the motion is not simple.
Try http://http://www.theorphys.science.ru.nl/people/fasolino/sub_java/pendula/doublependul-en.shtml

 

[Fabio010]

The diagram looks like no coupled pendulum arrangement I've ever seen.

You seem to have a rigid bar on the right - which could be a pendulum except that it has no mass associated.
On the left is another bar, this time with a mass so I assume that IS a pendulum. And between them you have a mass suspended on a cord.

The nearest thing to this in standard physics texts is two pendula coupled by a spring. The analysis of the motion is not simple.
Try http://http://www.theorphys.science.ru.nl/people/fasolino/sub_java/pendula/doublependul-en.shtml

that link is not working. :/

 

[Fabio010]

i found this equations to coupled pendulums.




I= inertial

α and β are angles.

M1 = mass of right pendulum
L1 = length of right pendulum = L2
m2 = mass of left pendl..

For the right pendulum:
I1.d^2α/dt^2 = -1/2.M1.g.L1.sinα - k[sinα - sinβ]

For the left pendulum:

I2.d^2β/dt^2 = -1/2.m2.g.L2.sinβ k[sinα - sinβ]



in the limit of small angles

α,β << 1
so:

I1.d^2α/dt^2 = -1/2.M1.g.L1.α - k[α-β]

I2.d^2β/dt^2 = -1/2.m2.g.L2.β + k[α-β]


if we consider a weak coupled pendulum system, then:

k<<1

and because left pendulum have a mass and a inertia much greater then the right pendulum:

M1>>m2 and I1>>I2

Equation to right pendulum can be simplified to:

I1.d^2α/dt^2 ≈ -1/2.M1.g.L1.α


to left pendulum we have:

I2.d^2β/dt^2 = -[1/2.m2.g.L2.β+ kβ ] + kα

i.e

I2.d^2β/dt^2 + (ωo)^2.β = kα(t)




then

(ωo)^2 = 1/2 * (m2gL2) + k

so the frequency induced by the right pendulum to the left pendulum is:

f = 2.pi/ωo ...

is that right?