FabledIntg
- 43
- 0
Thread moved from the technical forums, so no Homework Template is shown
I'm supposed to express the reultant force R of M, F1 and F2 in terms of F1, F2, r, s and α. But I need to know how to draw R first. How can one do this?
Does the couple create a force uppwards from O? Can I move F_1 and F_2 also to the origin and combine the forces?
Here is the image:
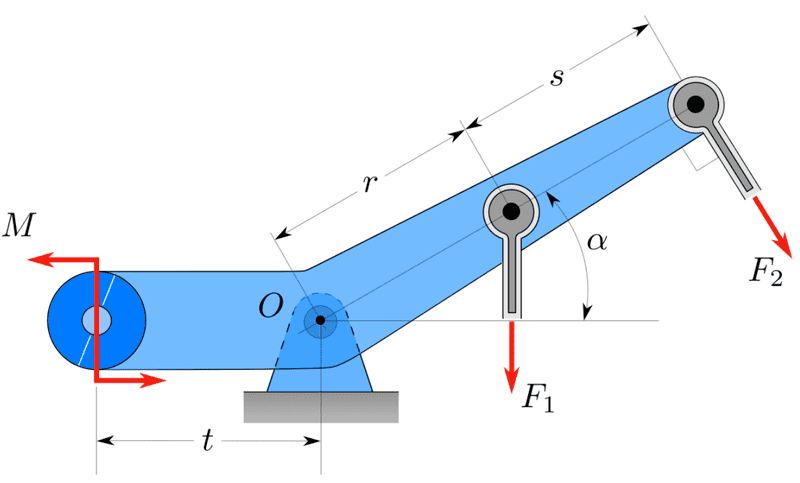
Does the couple create a force uppwards from O? Can I move F_1 and F_2 also to the origin and combine the forces?
Here is the image:
Attachments
Last edited: