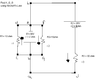
First, let's start with the basics. I don't know how you visualize circuits, but what helps me is to think of it as a system of pipes and water sources; let me explain.
Picture the voltage source (in this case you have two) as a water pump. It's purpose is to pump water through the pipe it is connected to. Think of a resistor as something in the pipe that slows the water down. So starting from your 20V "water pump" picture water being pumped out towards the 4\Omega resistor. The amount of water that is being pumped out is the current. In your diagram you lableled it I_3. So the amount of water, or I_3 is being pumped from the 20V voltage source. It hits the 4 \Omega resistor and changes speed, which means it changed voltage, NOT CURRENT. So The current across the 20V is the same across the 4 \Omega. This is the case for elements of a circuit in series. So let's just call this a rule:
1) The current across elements hooked up in series is equal.
So following along with our water analogy, you hit the 30 \Omega resistor. Again, the current is the same, the voltage is different. Next up we get to the "hard" part. The current comes in and hits the node you labled "b". Now what?
Well think of it like water. The water will go through all of those pipes right? But you only have so much water to move through them. So water will move to node "c" and travel to "d" and it will move to node "g" and travel to node "f", it will even move down the middle and travel from node "b" across "e". So this means you are actually going to have 4 different currents.
You didn't label the current from node "b" to "e" so let's do that now. We will call it I_0.
So now let's use kirchhoffs laws to solve the circuit.
First, what are they?
Well you have KVL, and KCL, or...
KVL = kirchhoffs voltage law
KCL = kirchhoffs current law
Let's start with KCL. KCL something along the lines of, the current that comes into a node must equal the current going out of that node.
So go back to the circuit and look at node "J" for a second. Remember we labeled this current I_3. Well you have I_3 coming into the node from the 30\Omega resistor side, and you also have I_3 leaving a side. So your expression for it would be:
I_3 = I_3.
This isn't very useful, as it doesn't yield any new information. So you really don't want to chose a node like that. Instead choose a node where more than one current is entering. And you happen to have two of them. Do you see why?
What are they?
Lets go back to KCL for a second. The general expression that I use to remember KCL is:
\sum i_{IN} = \sum i_{OUT}
That may or may not help you.
So back to the nodes. How many do you have? Yup... you have two:
Node B and Node E.
Lets look at Node E. What are the currents coming into it?
(You didn't label I_0, so let's say it is traveling "up" towards the 20V source. So back to Node E. You have the following:
I_3 comes in.
I_1 leaves.
I_0 leaves.
I_2 leaves.
Remember,
\sum i_{IN} = \sum i_{OUT}
So the expression would be:
I_3 +I_2 = I_1 + I_0.
Now you show me your steps for the other node.Now to KVL. KVL says something along the lines of, as you loop around the circuit the voltage drop across elements totals to 0. I remember it like this:
\sum v_i = 0
What is difficult here, is getting the polarity straight. It would be much easier to show this in person, but I'll try to explain. Let's just go through the example, and hopefully you will pick it up. First, let's define something though, that will hopefully make sense later.
A) If we are looping along in the direction of the current, a resistor will have a POSITIVE polarity.
B) If we are looping along in the opposite direction of the defined current, a resistor will have a NEGATIVE polarity.
C) If we loop into a voltage source, the polarity is given by which sign we touch, either (+) or (-).
So let's start our first loop. Start from the 20V source. We will start our loop just behind the element, and travel in the direction that we defined I_3. So we first touch the (+) side of the voltage source, so our expression thus far is:
20V + \cdot \cdot \cdot = 0.
Next we reach the 4 \Omega resistor and because of our rules we defined above, we know that when we reach a resistor when we are following the direction of the current we get a postive polarity, so our new expression is:
20V + (4\Omega)(I_3) \cdot \cdot \cdot = 0. Remember that we are summing up voltages, so from Ohm's law we have V=IR.
We reach the 30 \Omega [/tex] and get do the same:<br />
<br />
20V + (4\Omega)(I_3) + (30\Omega)(I_3) + \cdot \cdot \cdot = 0<br />
<br />
Now we keep looping and we get to the split. We can loop in three directions, down the middle, to the left, and to the right. Let's go down the middle.<br />
<br />
We first get to the 30V source, so because we hit the (+) side first we will continue with our expression and have:<br />
<br />
20V + (4\Omega)(I_3) +(30\Omega)(I_3) + 30V + \cdot \cdot \cdot = 0.<br />
<br />
Now we get to the 2 \Omega resistor. Remember that the current changed here, and we lableled it I_0. So we are not dealing with the I_3 current anymore, so our expression would be:<br />
<br />
20V + (4\Omega)(I_3) +(30\Omega)(I_3) + 30V + (2\Omega)(I_0)= 0<br />
<br />
So now you have two expressions:<br />
I_3 +I_2 = I_1 + I_0<br />
20V + (4\Omega)(I_3) +(30\Omega)(I_3) + 30V + (2\Omega)(I_0)= 0<br />
<br />
The two expressions have 4 unknowns, so you can't solve these yet. You are going to need some more expressions, so use KCL and KVL to finish it up and post your work on here.
is there a shortcut way to solve the current in a circuit using kirchhoffs law?? or... is there a law or other easiest solution that can solve the the current in a circuit?? because my prof. gave us the equation and solution, but it is too long to solve? hope u can help me...
