How can someone prove the following trigonometric identity?

[cocopops12]

it's bothering my brain..i thought about it many times...i can't make intuition of it
can anyone prove it?

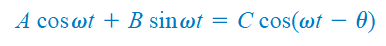
oh by the way... C = Sqrt[A^2 + B^2] and theta is equal to arctan(B/A)

 

[chiro]

Hey cocopops12 and welcome to the forums.

The easiest way IMO is to use geometry.

Think about for example right angled triangle with the hypotenuse coordinates (Bsin(wt),Acos(wt)).

Now think about the angles and sides involved where in your RHT, you have (Acos(wt))^2 + (Bsin(wt))^2 = hypotenuse.

 

[I like Serena]

Perhaps you could use the angle-difference-identity of the cosine?
See: http://en.wikipedia.org/wiki/Trig_identities#Angle_sum_and_difference_identities

That is: $\cos(ωt-θ)=\cos(ωt)\cos(θ) + \sin(ωt)\sin(θ)$.

@chiro: I don't understand how your triangle would work out...
However, I can think of different triangles that would fit.
You can draw 3 rectangular triangles with sides (A,B,√(A²+B²)), (Acos(ωt),Asin(ωt),A), and (Bcos(ωt),Bsin(ωt),B).
In the proper configuration these 3 triangles show the result.

 

[chiro]

Perhaps you could use the angle-difference-identity of the cosine?
See: http://en.wikipedia.org/wiki/Trig_identities#Angle_sum_and_difference_identities

That is: $\cos(ωt-θ)=\cos(ωt)\cos(θ) + \sin(ωt)\sin(θ)$.

@chiro: I don't understand how your triangle would work out...
However, I can think of different triangles that would fit.
You can draw 3 rectangular triangles with sides (A,B,√(A²+B²)), (Acos(ωt),Asin(ωt),A), and (Bcos(ωt),Bsin(ωt),B).
In the proper configuration these 3 triangles show the result.

Yeah that would be optimal.