How can we calculate the probability?

[mathmari]

Hey! :giggle:

The distribution of a random variable $X:\Omega\rightarrow \mathbb{R}$ is given by the probability function $p_X$ as follows:

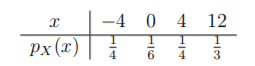
(i) Calculate the distribution function $F_X$ of $X$.
(ii) Let $Y(\omega)=|X(\omega)|$ for all $\omega\in \Omega$. Determine $p_Y$. I have done the following :

(i) \begin{align*}&F_X(-4)=p_X(-4)=\frac{1}{4} \\ &F_X(0)=p_X(-4)+p_X(0)=\frac{1}{4}+\frac{1}{6}=\frac{5}{12} \\ &F_X(4)=p_X(-4)+p_X(0)+p_X(4)=\frac{1}{4}+\frac{1}{6}+\frac{1}{4}=\frac{5}{12}+\frac{1}{4}=\frac{2}{3} \\ &F_X(12)=p_X(-4)+p_X(0)+p_X(4)+p_X(12)=\frac{1}{4}+\frac{1}{6}+\frac{1}{4}+\frac{1}{3}=\frac{2}{3}+\frac{1}{3}=1\end{align*}

(ii) We have that $Y(\Omega)\in \{0, 4, 12\}$, right? But how can we calculate the probability? :unsure:

 

[I like Serena]

(ii) We have that $Y(\Omega)\in \{0, 4, 12\}$, right? But how can we calculate the probability?

Hey mathmari!

Don't we have for $y\ge 0$ that $p_Y(y)=P(Y(\omega)=y)=P(|X(\omega)|=y)=P(X(\omega)=y \lor X(\omega)=-y)$?

Btw, we have for $\omega\in \Omega$ that $Y(\omega)\in \{0, 4, 12\}$.
However $Y(\Omega)= \{0, 4, 12\}$. (Nerd)

 

[mathmari]

Don't we have for $y\ge 0$ that $p_Y(y)=P(Y(\omega)=y)=P(|X(\omega)|=y)=P(X(\omega)=y \lor X(\omega)=-y)$?

Btw, we have for $\omega\in \Omega$ that $Y(\omega)\in \{0, 4, 12\}$.
However $Y(\Omega)= \{0, 4, 12\}$. (Nerd)

So we get $$p_Y(0)=\frac{1}{6}, \ p_Y(4)=\frac{1}{4}, \ p_Y(12)=\frac{1}{3}$$ right? :unsure:

 

[I like Serena]

So we get $$p_Y(0)=\frac{1}{6}, \ p_Y(4)=\frac{1}{4}, \ p_Y(12)=\frac{1}{3}$$ right?

They should sum up to 1...
It seems we missed a chance somewhere. (Worried)

 

[mathmari]

They should sum up to 1...
It seems we missed a chance somewhere. (Worried)

Do we maybe have the following :
$$p_Y(4)=P(X(\omega)=4 \lor X(\omega)=-4)=P(X(\omega)=4) + P(X(\omega)=-4)=\frac{1}{4}+\frac{1}{4}=\frac{2}{4}=\frac{1}{2}$$
:unsure:

 

[I like Serena]

Do we maybe have the following :
$$p_Y(4)=P(X(\omega)=4 \lor X(\omega)=-4)=P(X(\omega)=4) + P(X(\omega)=-4)=\frac{1}{4}+\frac{1}{4}=\frac{2}{4}=\frac{1}{2}$$

Yep. (Nod)

 

[mathmari]

Yep. (Nod)

So for all probabilities we have :
\begin{align*}p_Y(0)&=P(Y(\omega)=0)=P(|X(\omega)|=0)=P(X(\omega)=0 \lor X(\omega)=-0)=P(X(\omega)=0)\\ & = \frac{1}{6} \\
p_Y(4)&=P(Y(\omega)=4)=P(|X(\omega)|=4)=P(X(\omega)=4 \lor X(\omega)=-4)=P(X(\omega)=4) + P(X(\omega)=-4)\\ & =\frac{1}{4}+\frac{1}{4}=\frac{2}{4}=\frac{1}{2} \\
p_Y(12)&=P(Y(\omega)=12)=P(|X(\omega)|=12)=P(X(\omega)=12 \lor X(\omega)=-12)\\ & =P(X(\omega)=12) + P(X(\omega)=-12)=\frac{1}{3}+0=\frac{1}{3}\end{align*}
right? :unsure:

 

[I like Serena]

Yep. (Nod)

And they sum up to 1 now as they should.(Emo)

 

[mathmari]

Great! (Clapping)At the next subquestion we have :
Let $Z : \Omega \rightarrow \mathbb{R}$ be a random variable with distribution function $F_Z : \mathbb{R} \rightarrow [0, 1]$,

(i) Calculate $p_Z$.
(ii) Calculate $P[2 \leq Z < 3]$.I have done the following :

(i) \begin{align*}&p_Z(1)=F_Z(1)=\frac{2}{5} \\ &p_Z(2)=F_Z(2)-F_Z(1)=\frac{3}{5}-\frac{2}{5}=\frac{1}{5} \\ &p_Z\left (\frac{5}{2}\right )=F_Z\left (\frac{5}{2}\right )-F_Z(2)=\frac{9}{10}-\frac{3}{5}=\frac{9}{10}-\frac{6}{10}=\frac{3}{10} \\ &p_Z(3)=F_Z(3)-F_Z\left (\frac{5}{2}\right )=1-\frac{9}{10}=\frac{1}{10}\end{align*}

(ii) \begin{equation*}P[2\leq Z<3]=p_Z(2)=F_Z(2)-F_Z(1)=\frac{3}{5}-\frac{2}{5}=\frac{1}{5}\end{equation*} Is everything correct and complete? :unsure:

 

[I like Serena]

$Z$ is a continuous random variable now, which means we need to specify $p_Z$ for every real number.
What is for instance $p_Z(1.5)$? (Wondering)

 

[mathmari]

$Z$ is a continuous random variable now, which means we need to specify $p_Z$ for every real number.
What is for instance $p_Z(1.5)$? (Wondering)

Do you mean that we have to write :
\begin{align*}&p_Z(x)=F_Z(1)=\frac{2}{5} \ \text{ for } 1\leq x<2 \\ &p_Z(x)=F_Z(2)-F_Z(1)=\frac{3}{5}-\frac{2}{5}=\frac{1}{5} \ \text{ for } 2\leq x<\frac{5}{2} \\ &p_Z\left (x\right )=F_Z\left (\frac{5}{2}\right )-F_Z(2)=\frac{9}{10}-\frac{3}{5}=\frac{9}{10}-\frac{6}{10}=\frac{3}{10} \ \text{ for } \frac{5}{2}\leq x<3 \\ &p_Z(x)=F_Z(3)-F_Z\left (\frac{5}{2}\right )=1-\frac{9}{10}=\frac{1}{10} \ \text{ for } x>3 \end{align*} Or what do we do in this case? :unsure:

 

[I like Serena]

Do you mean that we have to write :
\begin{align*}&p_Z(x)=F_Z(1)=\frac{2}{5} \ \text{ for } 1\leq x<2 \\ &p_Z(x)=F_Z(2)-F_Z(1)=\frac{3}{5}-\frac{2}{5}=\frac{1}{5} \ \text{ for } 2\leq x<\frac{5}{2} \\ &p_Z\left (x\right )=F_Z\left (\frac{5}{2}\right )-F_Z(2)=\frac{9}{10}-\frac{3}{5}=\frac{9}{10}-\frac{6}{10}=\frac{3}{10} \ \text{ for } \frac{5}{2}\leq x<3 \\ &p_Z(x)=F_Z(3)-F_Z\left (\frac{5}{2}\right )=1-\frac{9}{10}=\frac{1}{10} \ \text{ for } x>3 \end{align*} Or what do we do in this case?

It's a bit strange really.
We have $F_Z(z) = \int_{-\infty}^z p_Z(x)\,dx \implies p_Z(x) = F_Z'(x)$.
That means that $p_Z(x)=0$ for $1<x<2$.
However, $F_Z(x)$ is not differentiable at $x=1$, so we would need to introduce the Dirac delta function to describe $p_Z(x)$ there.

 

[mathmari]

It's a bit strange really.
We have $F_Z(z) = \int_{-\infty}^z p_Z(x)\,dx \implies p_Z(x) = F_Z'(x)$.
That means that $p_Z(x)=0$ for $1<x<2$.
However, $F_Z(x)$ is not differentiable at $x=1$, so we would need to introduce that Dirac delta function to describe $p_Z(x)$ there.

Is this related to the below example?

:unsure:

 

[I like Serena]

Is this related to the below example?

Yes. That example shows $p_X$ as a discrete function and $F_X$ as a continuous function.
If we follow that example, then I think that what you wrote before for $p_Z$ as a discrete function is correct.

 

[mathmari]

Yes. That example shows $p_X$ as a discrete function and $F_X$ as a continuous function.
If we follow that example, then I think that what you wrote before for $p_Z$ as a discrete function is correct.

Do you mean what I wrote in post #9 or in post #11 ? :unsure:

 

[mathmari]

(ii) \begin{equation*}P[2\leq Z<3]=p_Z(2)=F_Z(2)-F_Z(1)=\frac{3}{5}-\frac{2}{5}=\frac{1}{5}\end{equation*}

I wrote all steps analytically as follows :
\begin{align*}P[2\leq Z<3]&=P[\{Z<3\}\setminus \{Z<2\}]=P[Z<3]-P[Z<2] \\ &=P[\{Z\leq 3\}\setminus \{Z=3\}]-P[\{Z\leq 2\}\setminus \{Z=2\}]\\ & =\left (P[Z\leq 3]-P[Z=3]\right )-\left (P[Z\leq 2]-P[Z=2]\right ) \\ &=\left (F_Z(3)-P[Z=3]\right )-\left (F_Z(2)-P[Z=2]\right )\\ &=\left (F_Z(3)-p_Z(3)\right )-\left (F_Z(2)-p_Z(2)\right )\\ &=\left (1-\frac{1}{10}\right )-\left (\frac{3}{5}-\frac{1}{5}\right )\\ &=1-\frac{1}{10}-\frac{3}{5}+\frac{1}{5}\\ & =\frac{1}{2}
\end{align*}
Are all steps correct? :unsure:

 

[I like Serena]

Do you mean what I wrote in post #9 or in post #11 ?

Post #9.

I wrote all steps analytically as follows :
\begin{align*}P[2\leq Z<3]&=P[\{Z<3\}\setminus \{Z<2\}]=P[Z<3]-P[Z<2] \\ &=P[\{Z\leq 3\}\setminus \{Z=3\}]-P[\{Z\leq 2\}\setminus \{Z=2\}]\\ & =\left (P[Z\leq 3]-P[Z=3]\right )-\left (P[Z\leq 2]-P[Z=2]\right ) \\ &=\left (F_Z(3)-P[Z=3]\right )-\left (F_Z(2)-P[Z=2]\right )\\ &=\left (F_Z(3)-p_Z(3)\right )-\left (F_Z(2)-p_Z(2)\right )\\ &=\left (1-\frac{1}{10}\right )-\left (\frac{3}{5}-\frac{1}{5}\right )\\ &=1-\frac{1}{10}-\frac{3}{5}+\frac{1}{5}\\ & =\frac{1}{2}
\end{align*}
Are all steps correct?

Correct although I believe it suffices to write:
\begin{align*}P[2\leq Z<3]= P(Z<3)-P(Z<2) =\lim_{x\to 3^-} F_Z(x) - \lim_{x\to 2^-} F_Z(x) = \frac 9{10}-\frac 25 =\frac{1}{2}
\end{align*}

 

[mathmari]

Post #9. Correct although I believe it suffices to write:
\begin{align*}P[2\leq Z<3]= P(Z<3)-P(Z<2) =\lim_{x\to 3^-} F_Z(x) - \lim_{x\to 2^-} F_Z(x) = \frac 9{10}-\frac 25 =\frac{1}{2}
\end{align*}

Ah ok! Thank you very much! (Sun)