How Can You Measure an Irregularly Shaped Tunnel's Area Over Time?

  • MHB
  • Thread starter Yankel
  • Start date
  • Tags
    Area
In summary, the individual is seeking a way to measure the changing area of a tunnel which does not have a defined shape. They can provide the distance between any two points and the width at various points along the length. They are considering using statistical methods such as monte carlo simulation to approximate the area. They are open to ideas for a practical measure.
  • #1
Yankel
395
0
Hello all

I have a tricky problem, maybe you can give me some ideas.

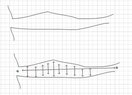
In the attached picture, there is a drawing of a shape, it is some sort of a tunnel, or channel.

This tunnel's area is varying in time, and I am looking for a way to measure it's area, so I can analyze the change over time. The problem is, it does not have a defined shape, not a geometric one, for area formulas, and not a functional one for the use of integrals or numerical evaluation of them.

What I CAN provide, is the distance between any two points in the tunnel. For instance, I can measure the length of the tunnel, approximately (!). I can also measure the width at any point, so basically I can measure the width at varying points, along the length (see arrows).

View attachment 1487

I am looking for a way to approximate the area of the tunnel, so I can know if it's "shrinking" or not. I was thinking maybe about statistical ways, like monte carlo simulation, but I am not sure I am even on the right direction here. Maybe you can give me some ideas for a practical measure ?

Thanks !
 

Attachments

  • Capture.JPG
    Capture.JPG
    15.6 KB · Views: 52
Mathematics news on Phys.org
  • #2
If you know the width at any point, or set of discrete places, then you can use any of the approximation methods for definite integrals.
 

FAQ: How Can You Measure an Irregularly Shaped Tunnel's Area Over Time?

1. What is "approximating irregular area"?

"Approximating irregular area" refers to the process of estimating the total surface area of a shape or object that does not have a regular, easily calculable shape. This can include complex shapes, curved edges, and irregular boundaries.

2. Why is approximating irregular area important?

Approximating irregular area is important in many scientific fields, such as engineering, architecture, and environmental science. It allows for accurate measurements of objects and landscapes, which can be used for planning, design, and analysis purposes.

3. What are some methods for approximating irregular area?

There are several methods for approximating irregular area, including the trapezoidal rule, Simpson's rule, and the Monte Carlo method. These methods use different mathematical formulas and algorithms to estimate the area based on known data points or randomly generated points within the shape.

4. How accurate are these methods for approximating irregular area?

The accuracy of these methods can vary depending on the complexity of the shape and the number of data points used. Generally, the more data points that are used, the more accurate the approximation will be. Some methods, such as the Monte Carlo method, can provide a more precise estimate but may require more computational power.

5. Are there any limitations to approximating irregular area?

Yes, there are limitations to approximating irregular area. These methods are based on estimations and assumptions, so they may not provide an exact measurement of the area. Additionally, the accuracy of the approximation can be affected by factors such as the shape's complexity, the quality of data points, and the chosen method.

Similar threads

B What is the Area of a Sierpinski Triangle?
Replies
7
Views
4K
I Creating a function with specific shape, intercepts, integral....
Replies
1
Views
990
MHB How Can You Calculate the Area of a Polygon Using Coordinates?
Replies
4
Views
2K
Area of a general n-sided polygon
Replies
4
Views
3K
I Work done by electric field of an irregularly shaped conductor
Replies
3
Views
1K
I The Basic Area Problem (introduction to the topic of integrals)
Replies
24
Views
3K
I Area under the curve of a temperature-time graph -> energy?
Replies
10
Views
2K
Best Tunnel Shape for X,Y,Z Coordinates
Replies
7
Views
3K
Exploring Wind Tunnel Data Collection Methods for Physics Coursework
Replies
1
Views
1K
MHB Is there a more reliable way to track a pulse in real time?
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top