How did they get this precession frequency of this gyroscope?

[unscientific]

To summarize:

1. The solenoid is supplied with an AC voltage.

2. Produces an AC magnetic field out of the page

3. Exerts an AC magnetic force on the Nb-Plate that's placed just outside of one end of the solenoid

4. There is a fluid circulating in the torus, with angular momentum L in the z-direction (out of the page)

5. What is the torque exerted on L due to the oscillating Nb-plate which forces the torus to oscillate with it?

Directions: ∅ (Left-right), θ (In-Out of page)

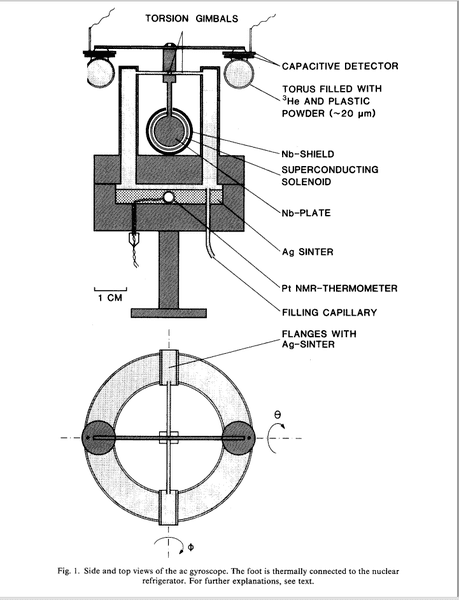
I'm not sure how they got an extra θ₀ term in their torque about ∅. I know in small oscillations, the magnitude of change in L is

ΔL ≈ θ₀L

Alternatively, considering change within half a period = T/2:

ΔL/Δt = 2θ₀L/T = 2fθ₀L

which also doesn't match their expression..

 

[256bits]

No response yet!

Which extra θ0 term are you referring to because I do not see an extra.

Also, are you not missing a pi term in
ΔL/Δt = 2θ0L/T = 2fθ0L

 

[unscientific]

No response yet!

Which extra θ0 term are you referring to because I do not see an extra.

Also, are you not missing a pi term in
ΔL/Δt = 2θ0L/T = 2fθ0L

Yeah, I did it two ways. Both don't match the expression they have derived..

 

[unscientific]

I think I know their line of thought, correct me if I'm wrong:

In time Δt, the vector (θ₀L) moves through an angle Δ∅. Hence

ΔL = (θ₀L)Δ∅

Taking limits of Δt → 0,

dL/dt = (θ₀)L(d∅/dt) = θ₀Lω_∅

 

[sardar]

I would approach this question by looking at the underlying principles and equations involved. The precession frequency of a gyroscope is determined by the torque acting on it, which is equal to the rate of change of its angular momentum. In this case, the torque is caused by the oscillating Nb-plate, which exerts an AC magnetic force on the torus due to the AC magnetic field produced by the solenoid.

To calculate the torque, we can use the equation τ = Iα, where τ is the torque, I is the moment of inertia, and α is the angular acceleration. The moment of inertia of the torus can be calculated using its geometry and mass distribution. The angular acceleration can be calculated using the equation α = Δω/Δt, where Δω is the change in angular velocity and Δt is the change in time.

In this system, the change in angular velocity is caused by the torque exerted by the oscillating Nb-plate. This torque can be calculated using the equation τ = r × F, where r is the distance from the axis of rotation to the point of application of the force, and F is the force acting on the object. In this case, the force is the magnetic force exerted by the oscillating Nb-plate.

By combining these equations and taking into account the direction and magnitude of the forces and torques, we can calculate the precession frequency of the gyroscope. The extra θ0 term in the torque expression may come from the specific geometry and orientation of the system, and would need to be further investigated and justified.

In summary, the precession frequency of the gyroscope is determined by the torque acting on it, which is caused by the oscillating Nb-plate exerting an AC magnetic force on the torus. By using the appropriate equations and considering the specific details of the system, we can calculate the precession frequency and explain the presence of any additional terms in the torque expression.