djMan
- 4
- 0
Homework Statement
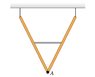
Two identical, uniform beams weighing 260 N each are connected at one end by a frictionless hinge. A light horizontal crossbar attached at the midpoints of the beams maintains an angle of 53.0 ∘ between the beams. The beams are suspended from the ceiling by vertical wires such that they form a "V", as shown in the figureWhat force does the crossbar exert on each beam?What is the magnitude of the force that the hinge at point A exerts on each beam?What is the direction of the force that the hinge at point A exerts on the right-hand beam?What is the direction of the force that the hinge at point A exerts on the left-hand beam?
Homework Equations
Ʃτ = 0
ƩF = 0
The Attempt at a Solution
I have tried to sum the torques and solve for the force of the bar however I end up getting a fraction with a zero numerator. I don't really know how to "see" this problem even after drawing it.