How do I calculate the speed of the Earth around the Barycentre with the Moon?

[darkdave3000]

I can find public information about the speed of the moon at max and min distance from the Earth (Ap vs Per) but how do I find the same information for the Earth's velocity around the same barycentre? The Earth's orbit around the barycentre is it a perfect circle or is it an ellipse? If it's an ellipse should I assumed that when the Moon is at max distance from the barycentre and the Earth that the same is true with the Earth's being at max distance from the said barycentre?

I can find some information about the distances both bodies should be from the barycentre here: https://en.wikipedia.org/wiki/Barycenter
But this assumes a circular orbit and not ellipsoid orbit that the Moon in reality orbits the Earth in. I assume this should also mean the Earth has an ellipsoid orbit around the same barycentre. Also this article gives no hints about the Earth's velocity at all around said barycentre.

How do I find out Earth's velocities at either extreme (Ap vs Per) of it's presumed ellipsoid orbit around the barycentre?

David

 

[Buzz Bloom]

How do I find out Earth's velocities at either extreme (Ap vs Per) of it's presumed ellipsoid orbit around the barycentre?

Hi dave:

I think the following Wikipedia article will be of some help.

https://en.wikipedia.org/wiki/Two-body_problem​

Regards,
Buzz

 

[darkdave3000]

So this will show me how to work out velocities at min and maximum distances of each body in an elliptical orbit? Great! Ill check it out and get back to you.

 

[jbriggs444]

You should be able to reason this out from first principles.

The barycenter is the center of gravity of the Earth plus moon. As you know, it will remain motionless [at least relative to its free fall orbital path around the sun, which is all we are concerned with].

In order for this to be true, the distance ratio of the two bodies from the barycenter must be in inverse proportion to their mass ratio. The mass ratio is fixed. So the distance ratio must be fixed as well. More generally, the two bodies must trace out identical orbits differing only in scale (in inverse proportion to the mass ratio).

You might imagine the arrangement as a sort of pantograph with the fixed pivot in the middle, the tracer on one end and a pencil on the other.

 

[sophiecentaur]

It may seem like stating the bleeding' obvious but these problems always require making (and writing down) an equation and solving it. Arm waving doesn't solve the problem.
No one has actually stated that:
v (of centre of mass) = angular velocity X radius of rotation. We know the two right hand terms so . .. . .
The Earth-Moon distance varies so neither orbit can be circular. There is very accurate information about the Earth-Moon distance so that gives Earths radius of orbit from simple lever calculations. The only bit of hard work is searching for the two bits of data to the accuracy that the OP wants.

 

[darkdave3000]

nssdc.gsfc.nasa.gov/planetary/factsheet/moonfact.html

From the above link I fed in some data into my simulation software using Runge Kutta and Improved Euler methods, both yielded a result where Earth and Moon slowly moved away from each other.

I had Moon at position X = 0km, Y = (405400-4671)km, Velocity: X = -0.970km/s
Earth X = 0km, Y = -4671km, Speed: X = 0.01193km/s
barycentre: X = 0, Y = 0

 

[darkdave3000]

Ignore the straight lines coming from Earth, their paths of a projectile simulation gone wrong. The large white circle centred on the Earth and stretches near the moon is just the average distance from Earth to the Moon so it's just a marker. The curvy lines are what you need to pay attention to as they trace out the orbits of Earth and Moon and turn from Green to Red gradually over the passage of time. The small white circle in the Earth is the barycentre.

 

[sophiecentaur]

yielded a result where Earth and Moon slowly moved away from each other.

I don't understand the mechanism that this is simulating. Unless you include tidal locking, why should the separation be increasing?
I can't see why the ratio of the speeds of the two bodies is not just inversely proportional to the ratio of their separation rom the BC. This has been spelled out by @jbriggs444 already. Is there some extra agenda here that you haven't mentioned?

 

[darkdave3000]

Agenda? I just want to achieve stable orbit. The mechanism is Newtonian physics, at each time increment(about 1/30th per second) the computer calculates the acceleration due to gravity of both objects to each other and adjusts the velocity and displacement accordingly. It's using Acceleration = Gm/r^2 and velocity = v+at and displacement = 1/2 at^2 + vt.

Basically Newtonian physics. The initial figures I used already spelled out above in km. And I get these results as seen in the screenshots. I tried adjusting the distance and speeds but they caused even more instability.

 

[darkdave3000]

I managed to improve results by decreasing the size of the time step down to a minute per increment. I guess once I get it down to a second the decay will disappear.

What do you think? Will General Relativity eliminate the decay completely?

David

 

[jbriggs444]

I managed to improve results by decreasing the size of the time step down to a minute per increment. I guess once I get it down to a second the decay will disappear.

What do you think? Will General Relativity eliminate the decay completely?

The orbital decay is a numerical problem resulting from your implementation of the model, not a problem with the model per se. There is no orbital decay (or acceleration) in the Newtonian model. Changing it out in favor of general relativity will not help.

 

[darkdave3000]

The orbital decay is a numerical problem resulting from your implementation of the model, not a problem with the model per se. There is no orbital decay (or acceleration) in the Newtonian model. Changing it out in favor of general relativity will not help.

But you know the moon is in fact getting further away 22mm per year.
https://en.wikipedia.org/wiki/Orbit_of_the_Moon#Tidal_evolution

What aspect of my implementation is causing the error otherwise? Is it because my time increments are still too big? (1 minute per jump). If so how small should I get it to eliminate the error?

Additionally the orbit of the moon it self also rotates once every 8 years, could the anomaly I'm seeing be a result of this rotation(precession of line of apsides)? Since I am now using real life data from the almanac could this aspect of the rotation be showing up as a decay? Implementing GR should show this rotation of the orbit right? A precession?

precession of line of apsides 8.8504 years

I read that General Relativity accounts for this precession:
https://en.wikipedia.org/wiki/Apsidal_precession#General_relativity

Anomaly from real life data I am talking about is:
The orbital speed at the moon's distance from Earth should be 1.03km/s but the moon is moving at 1.02km/s. Could this anomaly be what's causing the decay because my simulator doesn't use GR field equations to make the rotation rotate instead of decay?

 

[Vanadium 50]

What aspect of my implementation is causing the error otherwise?

Who knows?

But you know the moon is in fact getting further away 22mm per year.

The fact that an error in your implementation gives you an answer with the same direction (but wrong magnitude) as the true one might be helpful in finding it. It surely doesn't mean it's not there.

 

[Janus]

But you know the moon is in fact getting further away 22mm per year.
https://en.wikipedia.org/wiki/Orbit_of_the_Moon#Tidal_evolution

Since you are treating Earth and the Moon as point masses and not as objects that deform under gravity, your simulation would not reflect this. You would have to add further calculations to include this effect.

What aspect of my implementation is causing the error otherwise? Is it because my time increments are still too big? (1 minute per jump). If so how small should I get it to eliminate the error?

for perfect accuracy, they would have to be infinitely small. But barring that,small enough so that the error is something you can live with. The problem is that your calculation for each "jump" of a given time period can only approximate the actual motion. It's a lot like trying to find the circumference of a circle by calculating the perimeter of a polygon that the circle fits in. The more sides the polygon has, the closer you get to the circumference of the circle, but you never can get 100% accuracy

Additionally the orbit of the moon it self also rotates once every 8 years, could the anomaly I'm seeing be a result of this rotation? Since I am now using real life data from the almanac could this aspect of the rotation be showing up as a decay? Implementing GR should show this rotation of the orbit right? A precession?

precession of line of apsides 8.8504 years

Again, this is due to influences that your calcuations do not account for, most notably, the gravitational effect of the Sun.

I read that General Relativity accounts for this precession.

No, The precession of the Moon's orbit is primarily due to influence of the Sun. You are likely thinking of the precession of Mercury, which in part is due to GR. Mercury would still precess in its orbit due to the various tugs of the other planets, GR just adds a small additional amount. But this is only really noticeable because Mercury orbits so close to the Sun and has a fairly eccentric orbit. For the Moon orbiting the much smaller Earth and with nowhere near an eccentric orbit, any GR induced precession would be lost in any other inaccuracies in your numbers.

 

[darkdave3000]

Ok I have added the sun into the simulation. What this did was make the moon actually go the opposite direction but only slightly. So the moon is now falling toward the Earth(slightly). However when increasing the jump from 1 minute to 13.6 minutes the moon now looks like is falling away again however this is the jump I need to create a full Earth orbit which seems to be falling away from the Sun.

Have a look at the following screenshots.

How strange... why would the moon now be falling toward the Earth with all correct data including the Sun? Do I need to add in the gas giants too?

Merry Christmas Everybody!

Update: Ok the moon's orbit around the Earth is adjusted so it's always relative to the Earth's core, not the barycentre, so it's not so accurate. I'll run the sim again with the sun moving opposite to the Earth's velocity instead of being stationary while making Earth and Moon not move at Earth's speed. That way Ill be able to redraw the moon's orbit but relative to barycentre.

 

[darkdave3000]

Oh man, … with the sun in there I cannot keep track of the barycentre...

 

[Janus]

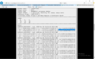
Ok I have added the sun into the simulation. What this did was make the moon actually go the opposite direction but only slightly. So the moon is now falling toward the Earth(slightly). However when increasing the jump from 1 minute to 13.6 minutes the moon now looks like is falling away again however this is the jump I need to create a full Earth orbit which seems to be falling away from the Sun.

Have a look at the following screenshots.

How strange... why would the moon now be falling toward the Earth with all correct data including the Sun? Do I need to add in the gas giants too?

Merry Christmas Everybody!

Update: Ok the moon's orbit around the Earth is adjusted so it's always relative to the Earth's core, not the barycentre, so it's not so accurate. I'll run the sim again with the sun moving opposite to the Earth's velocity instead of being stationary while making Earth and Moon not move at Earth's speed. That way Ill be able to redraw the moon's orbit but relative to barycentre.

That's not what you wanted to do. Adding the Sun just compounded the problem by adding extra factors when your original simulation wasn't even accurately modeling the simple scenario.

Earlier you said that you used 1/2 at^2 + vt. to calculate the displacement. But that will not give you the proper displacement for an orbiting object easily.

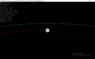
In the top image we show an object moving to the left at v with a downward acceleration of a downward. A simple application of the above equation will give you the displacement and new motion after some time t as shown in the second diagram. with the object following a parabolic path.

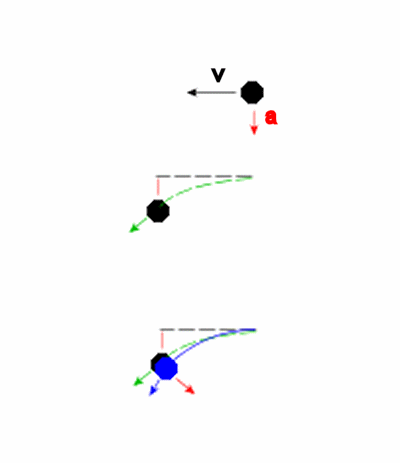
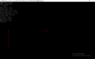
However, if the object is in an circular orbit ( where v is the circular orbital velocity) then it new position will be like the blue object in the bottom diagram and its path will be an arc of a circle. This is because, unlike the second diagram, which assumes that gravity acts in one direction the whole time, gravity really acts towards the center of the orbit which means by the end of the time period, it is pointing in the direction of the red arrow in the third diagram. With the Second diagram, the acceleration never effects v, and the final velocity is the vector sum of the velocity due to that acceleration and the original value of v and will end up being greater than v. In the third diagram, the direction of aceleration changes with respect to the original direction of v, and as a result the leftward component of the object's velocity will be less than the original v and it will end up that the new speed of the object, though in a different direction, will be of the same magnitude as the original v.
This error compounds with each time period even if at the end of each time period you reorient the direction of a to point towards the center of the planet.
Now, the smaller the time period you use, the smaller the difference between the two predicted paths. If you divide the above time period by ten, you get an much smaller deviation between the green and blue paths. So much smaller, that even after ten of these smaller time divisions, the total difference will still be smaller than when you used the one larger time period. This is why your simulation performed better when you used smaller time steps.

Orbital mechanics is just not a easy thing to figure out from the basics on up. Even Newton basically had to invent calculus in order to tackle it.

 

[darkdave3000]

My software recalculates acceleration due to gravity for every object relative to every other object per time increment. In other words acceleration vector updates as you said it should and constantly points toward the sum total of all gravitational influences after their position changes(or not).

The initial velocities of each planet and moon are factored in. The velocity is also updated every time increment by the formula "at + v".

Acceleration is updated by the Newtonian gravitational formula between all the masses, note at this point what happens is for each object, the acceleration vectors due to gravitational influence of every other object is calculated and added together and the sum total is the new acceleration for that particular object, this calculation is repeated for all objects. So the sun's acceleration is the sum total of two other acceleration vectors, one calculated for the Sun's pull by the Moon, the other by the Earth. The Earth's acceleration vector is the vector sum of the acceleration vectors calculated for the sun and the moon. And the moon's acceleration vector calculated by adding its acceleration to the sun and the Earth.Note displacement, velocity and acceleration are all vectors with direction and magnitude. The software also has many modes of using the above formulas, it can use Euler's method , Improved Euler's method, also Runge Kutta.

So does this sound right to you?

That's not what you wanted to do. Adding the Sun just compounded the problem by adding extra factors when your original simulation wasn't even accurately modeling the simple scenario.

Earlier you said that you used 1/2 at^2 + vt. to calculate the displacement. But that will not give you the proper displacement for an orbiting object easily.Orbital mechanics is just not a easy thing to figure out from the basics on up. Even Newton basically had to invent calculus in order to tackle it.