shreddinglicks
- 225
- 7
Homework Statement
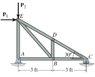
Determine the force in each member of the truss. State if the members are in tension or compression.
P1 = 450 lb, P2 = 600 lb
Homework Equations
The Attempt at a Solution
No matter what I try I get wrong answers. I need someone to get me going in the right direction.