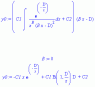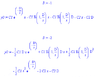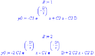How do I solve a 2nd order DE with constants a, b, c1, and c2?

[pothuri]

hi all...

i need to solve this differential equation of 2nd order...if anyone could tell me the way or method to use to do it i would appreciate it. i don't mind if the sol is given

a*x^2 y''+(bx-c1)*y'-by+c2=0

where y'=dy/dx and y"=d^2y/d^2x

a,b,c1,c2 are constants


thanx

 

[arildno]

You have probably seen that one of the solutions is linear: y1(x) =Ax+d,
where A and d satisfy the relation: A*c1+d*b=c2

For the second case, see if you can find a power series solution.

 

[pothuri]

u mean to say consider the homogeneous part of the equation and get a power series solution y2(x) ?...

 

[Dr Transport]

Try a series solution of the form \sum a_{l+m}x^{l+m} differentiate term by term, and then match coeficient of like powers of x^{l+m}.

 

[Max0526]

it's solvable

Hi, pothuri;

First of all, read all of these:
http://www.sosmath.com/diffeq/second/second.html.

Now, some clarification.

a*x^2*y''+(bx-c1)*y'-by+c2=0

This equation is a:

1) second order ODE. I mean I believe you are not interested in a solution for a particular case a=0. If so, why don't we divide the whole equation by a, and have the new constants: B=b/a, C1=c1/a, C2=c2/a.

2) non-homogeneous linear ODE. That means that you should solve the homogeneous part (without c2) first:
a*x^2*y''+(bx-c1)*y'-by=0,
or
x^2*y''+(Bx-C1)*y'-By=0.
In the case of second order linear homogeneous ODE the _general_ solution will be K1*y1(x)+K2*y2(x), where y1(x) and y2(x) are linear-independent solutions, K1, K2 - arbitrary constants.

So, to solve the equation
a*x^2*y''+(bx-c1)*y'-by+c2=0,
you first need to know at least one particular solution y1(x) for the equation
x^2*y''+(Bx-C1)*y'-By=0.

The equation
x^2*y''+(Bx-C1)*y'-By=0
is solvable (I solved it in Maple 9), but the form of its solution highly depends on the particular values of coefficients, especially B. Do you have any specific values for B=b/a and C1=c1/a now? If yes, can you post them? I didn't try any specific values yet, still I think the solution will have the simplest form under integer B, say B=+-1, +-2, +-3 (you don't need it under B=0, right?).

Sorry for not posting the solution right now, I don't have Maple installed on this machine, so I will post it later.

Best of luck,

Max.

 

[arildno]

Actually, you won't be able to find an ordinary power series solution to your problem (you might find a Frobenius series, though)
I'm sorry I led you astray.

If you read the link given by Max0526, the method I propose here will probably be included:

(I think it's called reduction of order)

Now for the second solution y2(x) (y1(x) is the linear solution Ax+B):

Make a trial solution y2(x)=f(x)y1(x)

You will gain a homogenous differential equation with only f''(x) and f'(x) present.
Hence, you can solve for f'(x) (you will need to use partial fractions decomposition).

f'(x) is determined up to an arbitrary constant C.
When you now integrate to find f(x), the usual constant of integration K may be set to zero.
The reason is:
Let F(x)=f(x)+K, (where f is the solution with the second integration set to zero)

Then, Y2(x)=F(x)y1(x)=f(x)y1(x)+ky1(x)=y2(x)+ky1(x).
Hence, Y2(x) is only a linear combination of the solutions y2(x) and y1(x).

 

[pothuri]

thanx everyone for replying...hey max,actually i have a bunch of values for the constants..i need to write a MATLAB program so that for each of these constants i need to find y depending on x. i don't have those values right now. if you want them i can get it.

and arildno i have tried the reduction of order method as u have said and ended up getting

f'(x)=x^a*e^(-b/x)/(Ax+B)^2

if i solve this i will get y2(x)...with y1(x) and y2(x) and using the method of variation of parameters provided in the link given by max..i can solve the original equation...am i goin in the right direction ?

will have to c how far i can solve the equation for f'(x)...

 

[arildno]

Don't thank me, I messed up something awful; my own "solution" was incorrect, and I believe your's is as well.
The reason is that, apart from the f', f'' terms, you'll end up with a term c2(1-f(x))
where I have used Ac1+Bb=c2.
Hence, my "method" didn't simplify at all..

 

[pothuri]

yeah even i got a more complicated one by substituting y2(x)=f(x)y1(x) in the original equation...but then i thought u were referring to the use of formula in the reduction of order method...i directly used the below formula ...its been 5yrs since i did some math

v'(x)=e^(-integral(P(x)dx))/y1(x)^2

then i tried to find out the y2(x)...i guess i am back to square one...

hey max can u post the solution in maple ... i will try if i can atleast use the output from urs into my program...

pavan

 

[pothuri]

i totally lost the way...actually i applied the reduction of order formula for the homogeneous equation and got the equation
f'(x)=x^B*e^(-C1/x)/(Lx+M)^2

the homogeneous equation is:
x^2*y''+(Bx-C1)*y'-By=0

=> y"+[(Bx-C1)/x^2]*y'-(B/x^2)*y=0

=> y"+P(x)y'+Q(x)*y=0 where P(x)=[(Bx-C1)/x^2] and Q(x)=-(B/x^2)

now for this y1(x) and y2(x) are the solution of which we can say that
y1(x)=Lx+M

now with y1(x) i used the reduction of order formula y2(x)=y1(x)*f(x)

where f'(x)=e^(-integral(P(x)dx))/y1(x)^2

after substitution of to get

f'(x)=x^B*e^(-C1/x)/(Lx+M)^2

if i find f and get y2(x)...i can use method of variation of parameters using y1 and y2 obtained from the homogeneous equation to solve the original equaiton..

am i still on the wrong way...if not i am not able to solve the equation for f'

f'(x)=x^B*e^(-C1/x)/(Lx+M)^2

waiting for replies...

 

[Max0526]

solutions

Well, guys, I'm terribly sorry for the delay.
The _general_ solution for the equation
x^2*y''+(B*x-D)*y'-By=0
(I changed C1 to D, Cn are usually integration constants)
is: (see y0BD.gif).
I provide you also with the solutions for B=0,+-1,+-2.
Maple 9 doesn't want to give the explicit solutions if B is not integer.
Best of luck,
Max.

 

[Max0526]

Definition of Ei(a,z)

This is a definition for Ei(a,z) used in solutions.
Max.