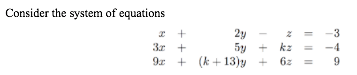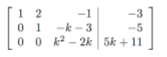MHB How Do Planes Intersect in Various Linear Systems?

[srg263]

Hi all,

I'm stuck on progressing a problem i have received some feedback around as detailed below. I would greatly appreciate some assistance, and thank you in advance for your time and contributions.

So i have a linear system:
View attachment 6673

Which is row reduced to:
View attachment 6674

I have identified that the system has no solutions for values of k = 0 or 2, and thus a unique solution if k does not equal 0 or 2.

I am stuck on the second part however which is:
"Each of these equations represents a plane. In each case (no solutions, infinitely many solutions or a unique solution, give a geometric description of the three planes."

I understand that:
*No solution = no common intersection of all thee planes
*Unique solution = three planes intersect in a single point
*Infinite solutions = intersection is either a plane or straight line.

I'm confused how to relate this to the systems of equations?

(Also apologies for the screen-shots, i cannot seem to get the maths symbol coding to work - any help with that would also be great!)

Many thanks mathematicians! :-)

 

[Euge]

Hello srg263,

If you've learned about rank, then considering that (in cases $k = 0, 2$) the coefficient matrix has rank 2 and the augmented matrix has rank 3, each plane intersects the other two planes in a line. If you haven't learned about rank, you can reach the same conclusion by considering the normals to the planes defined by the three equations. Indeed, the normals are coplanar (since the coefficient matrix has determinant $0$), but no two normals are multiples of each other (which implies that no two of the three planes are parallel). So again, each plane intersects the other two in a line.

 

[srg263]

Hello srg263,

If you've learned about rank, then considering that (in cases $k = 0, 2$) the coefficient matrix has rank 2 and the augmented matrix has rank 3, each plane intersects the other two planes in a line. If you haven't learned about rank, you can reach the same conclusion by considering the normals to the planes defined by the three equations. Indeed, the normals are coplanar (since the coefficient matrix has determinant $0$), but no two normals are multiples of each other (which implies that no two of the three planes are parallel). So again, each plane intersects the other two in a line.

Hi Euge,

Thank you for your response - i very much appreciate your time. Unfortunately i didn't quite understand your explanation there regarding the orientation of the planes that gives this solution set.

I was thinking drawing some diagrams might help me to understand, but I'm not really sure where to start.

Many thanks.

 

[I like Serena]

Let's start with the 3rd equation (in reduced form).
Which plane does it represent?

 

[Euge]

Hi Euge,

Thank you for your response - i very much appreciate your time. Unfortunately i didn't quite understand your explanation there regarding the orientation of the planes that gives this solution set.

I was thinking drawing some diagrams might help me to understand, but I'm not really sure where to start.

Many thanks.

Think of a triangular prism.

 

[srg263]

Let's start with the 3rd equation (in reduced form).
Which plane does it represent?

Thanks for your response.

Does it represent the z plane?

 

[I like Serena]

Thanks for your response.

Does it represent the z plane?

It represents a plane parallel to the z-plane, but only if there is at least 1 solution.

More specifically, the equation is:
$$(k^2-2k)z=11k+5$$
You already found that if $k^2-2k=0$, it has no solution.
And if $k^2-2k \ne 0$, we can write it as:
$$z=\frac{11k+5}{k^2-2k}$$
which is a plane parallel to the z-plane.

Which plane would the 2nd equation represent?