Engineering How Do You Calculate Apparent and Reactive Power in AC Circuits?

[charger9198]

For the circuit given in the power factor is 0.72 lagging and
the power dissipated is 375 W.

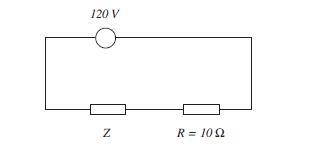
Determine the:
(1) apparent power
(2) reactive power
(3) the magnitude of the current flowing in the circuit
(4) the value of the impedance Z and state whether circuit is inductive or
capacitive.

(1) Apparent power = True power / Power Factor (S=P/pf)

= 375 / 0.72

= 520.8333 VA

(2) Reactive Power = SQRT (apparent power^2) - (True Power^2)

= SQRT (520.8333^2)-(375^2)

= SQRT (130642.3264)

= 361.4448 VAR

(3) Magnitude of Current

Power= Voltage*Current *Power factor (P=V*I*pf)

375 = 120*I*0.72
I = P/(V*pf)
I = 375/(120*0.72)
I = 4.34 A

(4) Total ohms = Voltage/Current
= 120/4.34
=27.6498 ohms (minus 10)
z = 17.65 ohms

The power factor is lagging within the circuit therefore the the virvuit is inductive



Am i on the right lines here? or is there a better way of calculating the above results

 

[gneill]

I find your calculation of total ohms (part 4) to be a bit dubious. Where you've made the assumption that you can just subtract the resistor value from the impedance magnitude to leave the impedance Z of the "mystery component" is also suspect. Impedance will have real and imaginary parts.

I'd be more inclined to use the current magnitude and its known phase angle obtained from the power factor to construct the complex current: i = I (cos(\phi) - j\;sin(\phi)), and then find the total (complex) impedance of the circuit:

Z_{tot} = \frac{120 V}{i} = (19.91 + j 19.19) \Omega

Then subtract the given resistor from the real part of that to leave the impedance Z.

 

[charger9198]

Ok thanks gneill

so ill use

ϕ=acos(power factor)
=acos (.72)
= 0.76699

then;

i = 4.34(cos(0.76699)-jsin(0.76699))
i = 4.339566
Zt=120/4.339566
=27.28723 (minus 10)
=17.28723

 

[gneill]

Ok thanks gneill

so ill use

ϕ=acos(power factor)
=acos (.72)
= 0.76699

then;

i = 4.34(cos(0.76699)-jsin(0.76699))
i = 4.339566 <---- This should be a complex value (real + imaginary components)
Zt=120/4.339566
=27.28723 (minus 10)
=17.28723

The complex current should retain real and imaginary components so that the impedance value obtained will also have real and imaginary components. These correspond to the resistance and reactance of the circuit.

 

[charger9198]

Think I've got it;

i=4.34(cos(0.76699)-jsin(0.76699)

i = 4.34(0.720003-0.693971)
i = (3.12481-3.01183j)

So

Z=120/(3.12481-3.01183j)

Z=19.9079 + 19.1882j

Minus ten from real gives

9.9079 ohms

This better? Are my answers ok for the other parts of the question?

 

[gneill]

Yes, that looks better. So the "mystery component" has both resistance and inductance.

The other answers look fine to me; nicely calculated.

 

[charger9198]

Thanks for you help as always :)

 

[gneill]

Thanks for you help as always :)

You're very welcome!

 

[stemurdo]

gneill said - I'd be more inclined to use the current magnitude and its known phase angle obtained from the power factor to construct the complex current: , and then find the total (complex) impedance of the circuit:



Charger said - ϕ=acos(power factor)
=acos (.72)
= 0.76699

I work the phase angle out at 43.95, where does this 0.76699 come from? I'm having a real problem getting my head round this 'imaginary' thing.

 

[gneill]

Charger said - ϕ=acos(power factor)
=acos (.72)
= 0.76699

I work the phase angle out at 43.95, where does this 0.76699 come from? I'm having a real problem getting my head round this 'imaginary' thing.

0.76699 is the angle in radians. You can work in degrees or radians as long as you're consistent.

 

[stemurdo]

ok so i use cos-1 x power factor, gives me a phase angle of 43.95 degrees.

i=I(cos(43.95)-jsin(43.95))
=4.34(cos(43.95)-jsin(43.95))
=4.34(0.7199-j0.694)
=(3.1244-j3.012)

is this right so far? this is where I'm getting a bit lost and not sure of the next step

 

[stemurdo]

am i right in saying that the jvalue is a negative value?
so it would actually be (3.1244 - (-3.012))
giving 120/6.134 = 19.555 for the real value? then how do you get the second jvalue?

 

[gneill]

am i right in saying that the jvalue is a negative value?
so it would actually be (3.1244 - (-3.012))
giving 120/6.134 = 19.555 for the real value? then how do you get the second jvalue?

You don't add the real and imaginary components of a complex number, they are separate entities. Take a look at post #5 in this thread. The impedance will have real and imaginary components, too.

 

[stemurdo]

sorry gneill, i can only ask for patience here. i appreciate the time.
i'm obviously missing something here, or just not grasping the concept at all!
if you don't add or subtract the jvalue then what purpose does it serve? how do you divide 120 by 3.124 and come up with 19.9 or whatever? my brain has packed up and gone home. :-)

 

[gneill]

sorry gneill, i can only ask for patience here. i appreciate the time.
i'm obviously missing something here, or just not grasping the concept at all!
if you don't add or subtract the jvalue then what purpose does it serve? how do you divide 120 by 3.124 and come up with 19.9 or whatever? my brain has packed up and gone home. :-)

You should review the manipulation of complex numbers; how to add, subtract, multiply, and divide them. http://www.allaboutcircuits.com/vol_2/chpt_2/6.html to get you started.

If you enter "Complex number arithmetic" into a Google search you'll get more information, and even links to online complex number calculators.

 

[terrytibbs]

Should the impedance be Vs/I which is 27.63 ohms. If there is an Inductance or Capacitance in the circuit the Z will be higher than R?

 

[gneill]

Should the impedance be Vs/I which is 27.63 ohms. If there is an Inductance or Capacitance in the circuit the Z will be higher than R?

27.63 Ω represents the magnitude of the impedance. Impedance is a complex value comprised of a real (resistive) and an imaginary (reactive) part. In this sense, yes, the magnitude will be greater than the size of the individual components: $|Z| = \sqrt{R^2 + X^2}$ . So for X nonzero, |Z| > R.

 

[mattyh3]

Think I've got it;

i=4.34(cos(0.76699)-jsin(0.76699)

i = 4.34(0.720003-0.693971)
i = (3.12481-3.01183j)

So

Z=120/(3.12481-3.01183j)

Z=19.9079 + 19.1882j

Minus ten from real gives

9.9079 ohms

This better? Are my answers ok for the other parts of the question?

i don't understand how get from Z=120/(3.12481-3.01183j) to Z=19.9079 + 19.1882j

can anyone explain this please if possible followed the link at the end but can understand from that how it get to Z=19.9079 + 19.1882j

 

[gneill]

i don't understand how get from Z=120/(3.12481-3.01183j) to Z=19.9079 + 19.1882j

can anyone explain this please if possible followed the link at the end but can understand from that how it get to Z=19.9079 + 19.1882j

It's basic complex arithmetic. You can convert the denominator to polar form (magnitude + angle) then do the division, convert the result back to rectangular form. Or, clear the imaginary term from the denominator by multiplying numerator and denominator by the complex conjugate of the denominator.

A web search on "complex arithmetic" will likely turn up a tutorial.

 

[mattyh3]

It's basic complex arithmetic. You can convert the denominator to polar form (magnitude + angle) then do the division, convert the result back to rectangular form. Or, clear the imaginary term from the denominator by multiplying numerator and denominator by the complex conjugate of the denominator.

A web search on "complex arithmetic" will likely turn up a tutorial.

you see none of this is in the lesson book for this course the only way i can find is z=v/i

there is polar form but nothing like what's on this page.. i still can't understand what your trying to tell me

just tried a complex arithmetic calculator online and i don't get them answers

 

[gneill]

you see none of this is in the lesson book for this course the only way i can find is z=v/i

there is polar form but nothing like what's on this page.. i still can't understand what your trying to tell me

just tried a complex arithmetic calculator online and i don't get them answers

Your course may assume that you've studied complex arithmetic in another course; It's generally taught in a mathematics course. If you haven't taken such a class, then you should find an online tutorial on complex numbers.

 

[mattyh3]

Should the impedance be Vs/I which is 27.63 ohms. If there is an Inductance or Capacitance in the circuit the Z will be higher than R?

well i thought it would be z=v/i but looks different on here and inductance becuase p.f is lagging

 

[mattyh3]

Your course may assume that you've studied complex arithmetic in another course; It's generally taught in a mathematics course. If you haven't taken such a class, then you should find an online tutorial on complex numbers.

i did a maths course before been aloud on this and there is nothing in there on this or how to do it

 

[gneill]

well i thought it would be z=v/i but looks different on here and inductance becuase p.f is lagging

Z = V/I is correct, assuming that V and I are complex values (well, here V is assumed to be the reference for the phasor angles, so V's imaginary component will be zero making V a real value). The I is determined from the given information using the power factor to determine the apparent current in complex form.

 

[mattyh3]

still can't find anything of any use that i can understand where the 120 goes and you end up with 19.9079+19.1882j

 

[gneill]

still can't find anything of any use that i can understand where the 120 goes and you end up with 19.9079+19.1882j

It's just division. A real number, 120, is being divided by the complex number 3.12481-3.01183j .

 

[mattyh3]

It's just division. A real number, 120, is being divided by the complex number 3.12481-3.01183j .

if i divide them into 120 it get 38.402+39.843j i don't understand any other way of doing it as am not great with maths

 

[gneill]

if i divide them into 120 it get 38.402+39.843j i don't understand any other way of doing it as am not great with maths

You'll have to find a complex number / complex arithmetic tutorial to learn about it. Or make use of an online complex arithmetic calculator (although that won't help you in tests or exams!).

Here's an example online calculator (found with via google with a couple of seconds effort):

http://www.1728.org/compnumb.htm

 

[mattyh3]

You'll have to find a complex number / complex arithmetic tutorial to learn about it. Or make use of an online complex arithmetic calculator (although that won't help you in tests or exams!).

Here's an example online calculator (found with via google with a couple of seconds effort):

http://www.1728.org/compnumb.htm

thanks for the help but i can't even use the calculator it gives me weird answers nothing like what's on here

this is what i get 19.408277013161786 + i*19.70643553618951

 

[gneill]

thanks for the help but i can't even use the calculator it gives me weird answers nothing like what's on here

this is what i get 19.408277013161786 + i*19.70643553618951

Yes, and that's the correct result for the impedance. It's a complex number with real and imaginary parts.